Задача 1:
Решить уравнение
ctg ²x = sin ²x + [ cos ²x],
где y и [y] — соответственно дробная и целая части числа y.
Задача 2:
Двое игроков по очереди вписывают в прямоугольную таблицу
1993 × 1994 (1994 столбца) числа 0 или 1. Потом находят суммы
чисел каждой строки и каждого столбца. Пусть S
1 — наибольшая
среди сумм по строкам, а S
2 — наибольшая среди сумм по столбцам.
Если S
1 > S
2, то выигрывает первый, а если S
2 ≥ S
1, то
выигрывает второй. Кто выиграет при правильной игре – начинающий
игру или его партнёр?
Задача 3:
Функция f(x) определена на множестве натуральных чисел и
принимает натуральные значения. Следует ли из справедливости
равенства f(x + y) = f(f(x) + f(y)) для любых x и y, что всегда
f(x + y) = f(x + f(y))?
Задача 4:
В треугольнике ABC углы A и B равны 72.
Биссектриса AN и медиана AM пересекают биссектрису BL в точках
E и D соответственно. Доказать, что LD • LE = ED • LB.
Задача 5:
Доказать, что для положительных чисел a, b и c значение
выражения a²b + b²c + c²a не больше хотя бы одного из чисел ab² + bc² + ca² и a³ + b³ + c³.
Задача 6:
Две прямые разбивают квадрат на четыре фигуры равной площади.
Доказать, что точки пересечения этих прямых со сторонами квадрата являются
вершинами нового квадрата.
Задача 7:
Построить многочлен с целыми коэффициентами (не равный
тождественно нулю), одним из корней которого является число
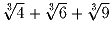
.
Задача 8:
Существует ли выпуклый пятиугольник F, отличный от
правильного, такой, что пятиугольник G, вершинами которого являются
внутренние точки пересечения диагоналей F, подобен пятиугольнику
F?


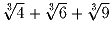 .
.