 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1993, Ровно >> 11 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1993, Ровно. 11 класс |
|
|
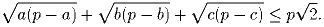
Задача 3: На плоскости заданы 2n точек (n — натуральное число). Двое игроков по очереди выбирают по одной точке до тех пор, пока точки не закончатся. Проигрывает тот, у кого сумма расстояний между выбранными им точками меньше, чем соответствующая сумма соперника. Может ли кто-то из игроков обеспечить себе выигрыш? (Считать, что все расстояния между данными точками и все суммы расстояний в разных группах точек попарно различны).
Задача 4: Даны две перпендикулярные скрещивающиеся прямые a и b. Они пересекают три данные различные параллельные плоскости соответственно в точках A1 и B1, A2 и B2, A3 и B3. Доказать, что три сферы, построенные на отрезках A1B1, A2B2 и A3B3 как на диаметрах, пересекаются по одной окружности.
Задача 5: Известно, что x и y –действительные числа, удовлетворяющие условию x + y = 1. Какое наименьшее значение может принимать выражение

Задача 6: На числовой прямой каждой целой точке поставлено в соответствие некоторое действительное число, причём точке 0 соответствует число 1,993. Доказать, что для некоторых 100 различных точек модуль суммы соответствующих им чисел больше 1.
Задача 7: Даны две разных касающихся окружности. В большей проводится произвольный диаметр AB и рассматриваются длины касательных, проведенных из точки A к меньшей окружности и из точки B к меньшей окружности. Доказать, что сумма квадратов длин этих касательных не зависит от выбора диаметра AB.
Задача 8: В языке племени Мумбо-Юмбо используются только две буквы — М и Ю. Все слова состоят ровно из 11 букв. Два слова считаются одинаковыми тогда и только тогда, когда они имеют одинаковые буквы более чем на пяти местах. Какое наибольшее количество разных слов может быть в языке племени Мумбо-Юмбо?
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1993, Ровно >> 11 класс | Показать решения |