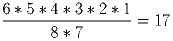Задача 1: В выражении

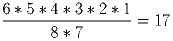
расставить вместо звёздочек знаки « + » или « – » так, чтобы получилось верное равенство.

Задача 2: Пусть S(n) — сумма цифр натурального числа n. Решить уравнение в целых числах: а) n² + S²(n) = 1993; б) n² + S²(n) = 2000.

Задача 3: При помощи циркуля и линейки восстановить треугольник ABC по его вершине A, середине стороны BC и основанию перпендикуляра, опущенного из точки B на биссектрису угла BAC.

Задача 4: Точка B — вершина равнобедренного треугольника ABC. Окружность S с центром в точке O касается прямой BC в точке B и продолжения стороны AC за точку C в точке D. Доказать, что точка пересечения прямых AB и OD лежит на окружности S.

Задача 5: Пусть a, b, c — целые числа и a + b + c = 1. Доказать, что (a + bc)(b + ac)(c + ab) — квадрат целого числа.

Задача 6: В каждой клеточке таблицы 8 × 8 записаны единицы. За один шаг разрешается выбрать в таблице произвольный квадрат 3 × 3 и увеличить на 1 каждое число выбранного квадрата. Доказать, что после 33 таких шагов в таблице можно будет найти квадрат 4 × 4, в четырёх угловых клетках которого стоят числа, дающие в сумме 37.