 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1994, Херсон >> 9 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1994, Херсон. 9 класс |
|
|
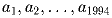 известно, что сумма любых пяти
из них, стоящих подряд, положительна. Обязательно ли положительна
сумма всех чисел?
известно, что сумма любых пяти
из них, стоящих подряд, положительна. Обязательно ли положительна
сумма всех чисел?Задача 2: Найти наибольшее возможное значение выражения
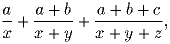
Задача 3: Можно ли прямоугольник размерами а) 1994 × 4 б) 1994 × 6
замостить плитками домино так, чтобы каждая прямая, пересекающая прямоугольник, пересекала хотя бы одну плитку домино?
Задача 4: Биссектрисы внешних углов выпуклого четырёхугольника в пересечении образуют новый четырёхугольник. Доказать, что сумма его диагоналей не меньше периметра исходного четырёхугольника.
Задача 5: Существует ли бесконечная арифметическая прогрессия, состоящая из различных простых чисел?
Задача 6: Внутри остроугольного треугольника ABC взята точка D такая, что ∠ ADB = 180 – ∠ ABC, а ∠ ADC = 180 – ∠ ACB. Доказать, что D лежит на медиане треугольника, проведенной к стороне BC.
Задача 7: Сравнить числа
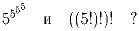
Задача 8: На плоскости дан выпуклый многоугольник и точка O внутри него. Доказать, что для любого натурального числа n > 1 на границе многоугольника найдётся n точек
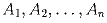 таких, что сумма
векторов
таких, что сумма
векторов 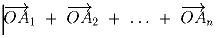 равна
равна 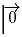 .
.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1994, Херсон >> 9 класс | Показать решения |