 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Чётность | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Чётность |
|
|
Решение: Нет. Звенья должны разбиваться на пары пересекающихся Задача 2: Может ли вращаться система из 11 шестеренок, если 1-я сцеплена со 2-й, 2-я – с 3-й и так далее, а 11-я сцеплена с 1-й?
Решение: Нет. Направления вращения шестерёнок должны чередоваться
Задача 3: Может ли прямая, не содержащая вершин 1001-угольника, пересекать каждую его сторону?
Решение: Нет. Любые соседние две вершины 1001-угольника должны лежать по разные стороны от прямой.
Задача 4: На клетчатой бумаге нарисован замкнутый путь (по линиям сетки). Доказать, что он имеет четную длину (сторона клетки имеет длину 1)
Решение: При прохождении пути шагов вверх должно быть столько же, сколько шагов вниз, а шагов вправо – столько же, сколько шагов влево. Задача 5: Улитка ползет по плоскости с постоянной скоростью, поворачивая на 90 градусов каждые 15 минут. Доказать, что она может вернуться в исходную точку только через целое число часов. Решение: Вправо улитка должна ползти столько же времени, сколько влево, а вверх – столько же, сколько вниз. Значит улитка проползла чётное число вертикальных и чётное число горизонтальных «пятнадцатиминутных» отрезков. К тому же вертикальные и горизонтальные отрезки чередуются, значит общее их число делится на 4.
Задача 6: Доказать, что любая ось симметрии 45-угольника проходит через его вершину.
Задача 7: Может ли кузнечик за 25 прыжков вернуться в начальную позицию, если он прыгает:
a) по прямой в любую сторону на нечетное расстояние.
b) по плоскости на расстояние 1 в любом из 4 основных направлений (вверх, вниз, вправо, влево)
с) по плоскости ходом коня (т.е. по диагонали прямоугольника 1 × 2).
d) по диагонали прямоугольника a × b (a и b фиксированы).
Решение: d) Нет. Если a и b оба нечётны, то каждая координата кузнечика при прыжке меняет чётность. Если же одно из чисел a и b чётно, а другое нечётно, то сумма координат при каждом прыжке меняет чётность. Если же a и b оба чётны, то можно уменьшать их вдвое до тех пор, пока одно из них не станет нечётным, а после этого воспользоваться одним из уже разобранных случаев. Задача 8: Кузнечик прыгает по прямой: первый раз – на 1 см, второй раз – на 2 см и так далее. Может ли он через 25 прыжков вернуться на старое место?
Задача 9: Четно или нечетно число 1 + 2 + 3 + … + 1990?
Задача 10: Набор домино выложили в ряд по правилам. На одном конце цепочки – пятерка. Что на другом?
Решение: Тоже пятёрка. Пятёрки внутри цепочки разбиваются на пары.
Задача 11: Из набора домино выкинули все кости с пустышками. Можно ли оставшиеся выложить в ряд по правилам?
Задача 12: В выражении 1*2*3* … *9 звездочки заменяют на – или +
a) Может ли получиться 0?
b) Может ли получиться 1?
c) Какие числа могут получиться?
Решение: c) Все нечётные числа от – 45 до 45.
Задача 13: У каждого марсианина три руки. Могут ли 7 марсиан взяться за руки?
Задача 14: Произведение
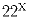 чисел 1 и – 1 равно 1.
Доказать, что их сумма не равна нулю.
чисел 1 и – 1 равно 1.
Доказать, что их сумма не равна нулю.
Задача 15: Может ли 25-звенная ломаная пересекать каждое свое звено по 3 раза?
Решение: Нет. Попытайтесь подсчитать количество точек пересечения. Задача 16: Можно ли стороны и диагонали правильного 13-угольника раскрасить в 12 цветов так, чтобы в любой вершине сходились все цвета?
Задача 17: На доске 25 × 25 расставлены 25 фишек, причем их расположение симметрично относительно обеих главных диагоналей. Доказать, что одна из фишек стоит в центре.
Задача 18: Доска 9 × 9 раскрашена в 9 цветов, причем раскраска симметрична относительно главной диагонали. Доказать, что на этой диагонали все клетки раскрашены в разные цвета.
Решение: Проще доказывать, что каждый цвет встречается на диагонали. Задача 19: На шахматной доске стоят 8 ладей, которые не бьют друг друга. Доказать, что число ладей, стоящих на черных клетках, четно.
Решение: Цвет клетки определяется суммой её координат. Сумма же координат всех ладей чётна (она не зависит от расстановки и равна 2(1 + 2 + … 8)).
Задача 20: Три кузнечика играют в чехарду: каждую секунду один из них прыгает через какого-то другого (но не через двух). Могут ли они через 25 секунд вернуться на свои места?
Задача 21: По окружности стоят 239 точек двух цветов. Доказать, что найдутся две точки одного цвета, разделенные ровно двумя точками.
Задача 22: В вершинах куба написаны числа 1 и – 1. На каждой грани написано произведение чисел в углах этой грани. Может ли сумма всех написанных чисел быть равна нулю?
Решение: Нет. Чисел всего 14, а их произведение равно 1. Задача 23: В таблице 25 × 25 расставлены целые числа так, что в каждом столбце и в каждой строчке встречаются все числа от 1 до 25. При этом таблица симметрична относительно главной диагонали. Доказать, что на главной диагонали все числа от 1 до 25 встречаются по одному разу.
Задача 24: n рыцарей из двух враждующих стран сидят за круглым столом. Число пар соседей-друзей равно числу пар соседей-врагов. Доказать, что n делится на 4.
Решение: Число пар соседей-врагов всегда чётно.
Задача 25: По кругу написаны 4 единицы и 5 нулей. За ход между двумя одинаковыми цифрами пишется единица, а между разными – ноль (старые цифры стираются). Могут ли через несколько ходов все числа стать одинаковыми?
Решение: Нет. Из чего могла получиться такая позиция?
Задача 26: В квадрате 25 × 25 стоят числа 1 и – 1. Вычислили все произведения этих чисел по строкам и по столбцам. Доказать, что сумма этих произведений не равна нулю.
Задача 27: По кругу расставлены нули и единицы (и те и другие присутствуют). Каждое число, у которого два соседа одинаковы, заменяют на ноль, а остальные числа – на единицы, и такую операцию проделывают несколько раз.
a) могут ли все числа стать нулями, если их 13 штук?
b) могут ли все числа стать единицами, если их 14 штук?
Задача 28: В вершинах n-угольника стоят числа 1 и – 1. На каждой стороне написано произведение чисел на ее концах. Оказалось, что сумма чисел на сторонах равна нулю. Доказать, что a) n четно b) n делится на 4.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Чётность | Убрать решения |