 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Уравнения в целых числах | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Уравнения в целых числах |
|
|
Задача 2: Найти все такие p, что p,p + 10 и p + 14 – простые. Решение: По модулю 3 Задача 3: Найти все такие p, что p и p² + 2 – простые. Решение: По модулю 3 Задача 4: Является ли число 12345678926 квадратом?
Задача 5: Доказать, что следующие числа не являются квадратами: a) 12345678 b) 987654 c) 1234560 d) 98765445.
Задача 6: Доказать, что 1 • 2 • 3 + 2 • 3 • 4 + … + 98 • 99 • 100 ≠ 19891988.
Задача 7: Найти все p, такие что p, p² + 4, p² + 6 – простые числа. Решение: По модулю 5 Задача 8: Доказать, что n4 + 2n² + 3 не может быть простым.
Решение: Оно делится на 3. Задача 9: Доказать, что число 2 + 4 + 6 + … + 2n не может быть
a) квадратом
b) кубом целого числа.
Задача 10: Решить в целых числах: 2x + 5y = xy – 1.
Задача 11: Найти все p, такие что p и p6 + 6 – простые.
Решение: По модулю 7 Задача 12: Найти все p, такие что p и 3p² + 1 – простые
Задача 13: Найти все p, такие что p и 2p² + 1 – простые.
Задача 14: Доказать, что произведение 6 последовательных натуральных чисел не может быть равно 776965920.
Задача 15: Доказать, что уравнение x² + 1990 = y² не имеет решений в целых числах.
Задача 16: Доказать, что уравнение 4k – 4l = 10n не имеет решений в целых числах. Решение: По модулю 3
Задача 17: Доказать, что существует бесконечно много натуральных чисел, не представимых в виде a) x² + y² b) x² + y² + z² c) x³ + y³ + z³. Решение: b) Все числа вида 8k + 7.
c) Все числа вида 9k + 4.
Задача 18: Доказать, что число 53 • 83 • 109 + 40 • 66 • 96 – составное.Задача 19: Решить в целых числах: x² + y² + z² = 4(xy + yz + zx).
Решение:
Метож бесконечного спуска: все переменные должны быть чётными и их можно разделить пополам. Ответ: (0;0;0)
Задача 20: Решить в целых числах: x² + y² + z² = 2xyz. Решение: Метод бесконечного спуска. Задача 21: Решить в целых числах: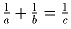
,
b и c – простые.Задача 22: Найти все прямоугольники с натуральными сторонами, у которых периметр равен площади.
Задача 23: Есть 100 купюр
типов: по a и b рублей. (a
не равно b). Доказать, что можно выбрать несколько купюр так,
что полученная сумма делится на 101 рубль без остатка.Задача 24: a) Решить в целых числах:
.
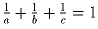b)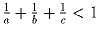 
.
Доказать, что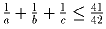 
.
Задача 25: Доказать, что существует бесконечно много натуральных чисел, не представимых в виде n² + p (p – простое). Решение:
Таковы почти все точные квадраты.
Задача 26: Доказать, что 32n – 1a) делится на 2n + 2.
b) не делится на 2n + 3.
Задача 27: Найти все натуральные n, для которых 2n + 33 – точный квадрат.
Задача 28: Решить в целых числах: a² + b² = 3(c² + d²).
Решение: Бесконечный спуск.
Задача 29: Найти наименьшее значение выражения
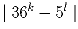(k, l – натуральные числа).
Решение: Ответ: 11 = 16 – 25. По модулям 3, 4 и 5.
Задача 30: Решить в простых числах: pqr = 7(p + q + r).
Задача 31: Решить в натуральных числах: 3N + 55 = m².
Задача 32: Решить в натуральных числах: 1 + x + x² + x³ = 2y.
Задача 33: Решить в целых числах: 5x³ + 11y³ + 13z³ = 0.
Задача 34: Решить в натуральных числах:
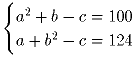.Задача 35: Разложить на множители: x³ + y³ + z³ – 3xyz.
Решение:
x³ + y³ + z³ – 3xyz делится на x + y + z. Найдите частное.
Задача 36: a – фиксированное натуральное число. Доказать, что уравнение x! = y² + a² имеет лишь конечное число решений (x,y).
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Уравнения в целых числах | Убрать решения |