 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Принцип Дирихле | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Принцип Дирихле |
|
|
Решение: Нет. Вертикалей, горизонталей и диагоналей всего 14, а возможных сумм – 13 ( от – 6 до 6).
Задача 2: За круглым столом сидят 100 человек, из них 51 – лысые. Доказать, что какие-то двое лысых сидят друг напротив друга.
Задача 3: Можно ли в таблице 6 × 6 расставить числа 0, 1 и – 1 так, чтобы все суммы чисел по вертикалям, горизонталям и двум главным диагоналям были различны?
Задача 4: 21 человек собрали 200 орехов. Доказать, что есть двое, собравшие поровну орехов.
Решение: Если у всех разное число орехов, то всего орехов не меньше чем 0 + 1 + 2 + … + 20 = 210. Задача 5: Доказать, что среди любых одиннадцати целых чисел найдутся два, разность которых делится на 10.
Решение: Есть два числа с одинаковой последней цифрой.
Задача 6: В некотором клубе у всех членов разное число волос. При этом членов в нем больше, чем число волос у любого, и нет человека, у которого ровно 100 волос. Каково наибольшее количество человек в таком клубе?
Решение: 100
Задача 7: Доказать, что из любых 1990 целых чисел найдутся два, разность которых делится на 1989.
Решение: Есть два числа с одинаковым остатком от деления на 1989 1989 Задача 8: Доказать, что найдется число вида 11 … 100 … 0, кратное 1989.
Решение: Среди чисел вида 11 … 1 есть два числа с одинаковым остатком от деления на 1989. Задача 9: Доказать, что в любом выпуклом многоугольнике найдутся две грани с одинаковым числом ребер.
Задача 10: Имеется 30 человек, некоторые из них знакомы. Доказать, что
a) есть два человека, имеющие одинаковое число знакомых.
b) если имеется только два человека с одинаковым числом знакомых, то есть ровно один, знакомый со всеми, или ровно один, не знакомый ни с кем.
Решение: Все количества знакомых должны лежать в интервале от 0 до 28 или в интервале от 1 до 29 (0 и 29 несовместны). Задача 11: 10 команд играют в турнир в один круг. Доказать, что в любой момент найдутся две команды, сыгравшие одинаковое число игр. Решение: Все количества игр каждой команды должны лежать в интервале от 0 до 8 или в интервале от 1 до 9 (0 и 9 несовместны). Задача 12: На единичной окружности закрашено несколько дуг с суммой длин больше π . Доказать, что найдутся две противоположные закрашенные точки.
Задача 13: На планете Тау Кита суша занимает больше половины всей площади. Доказать, что таукитяне могут прорыть через центр планеты шахту, соединяющую сушу с сушей.
Решение: Суша и область напротив суши перекрываются. Задача 14: В узлах клетчатой плоскости отмечено 5 точек. Доказать, что есть две из них, середина отрезка между которыми тоже попадает в узел.
Задача 15: Сумма 123 чисел равна 3813. Доказать что из этих чисел можно выбрать 100 с суммой не меньше 3100.
Задача 16: В ряд выписано 100 натуральных чисел. Доказать, что найдутся несколько подряд, сумма которых делится на 100.
Решение: Рассмотрите суммы чисел начальных отрезков этого ряда (точнее, их остатки по модулю 100).
Задача 17: a) Доказать, что есть две степени тройки, разность которых делится на 1000.
b) Доказать, что существует степень тройки, которая оканчивается на 0001.
Задача 18: Доказать, что найдется число вида
a) 1989 … 19890 … 0, делящееся на 1988.
b) 1988 … 1988, делящееся на 1989.
Задача 19: Из чисел от 1 до 200 выбрали 101 число. Доказать, что среди них есть два, одно из которых делится на другое.
Решение: Разбейте числа от 1 до 200 на 100 групп, в каждой из которых все числа делятся друг на друга. Задача 20: Доказать, что среди любых 13 чисел найдутся два, сумма или разность которых делится на 23.
Задача 21: На дереве 15 листьев. Доказать, что можно сорвать 8 из них так, что оставшиеся дают не меньше
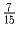 исходной тени.
исходной тени.Решение: Сведите задачу к случаю, когда тени листьев не перекрываются
Задача 22: Рыцарь едет по стране, поворачивая на развилках по очереди то направо, то налево. Доказать, что когда-нибудь он вернется в начало пути.
Задача 23: Строят башню из черных и белых кубиков, в основании которой лежит прямоугольник 3 × 4. Первый слой – произвольный, каждый следующий кладется так, чтобы любой кубик в предыдущем имел четное число черных соседей. Доказать, что когда-нибудь встретится слой, целиком состоящий из белых кубиков.
Решение: Легко доказать, что раскраски слоёв «зацикливаются». Кроме того, можно считать, что имеется целиком белый «нулевой» слой. Задача 24: Есть 20 гирь, каждая по целому числу граммов, суммарный вес которых не больше тонны. Доказать, что из них можно выбрать две (непересекающиеся) группы равного веса.
Решение: Сколько всего наборов из 20 гирь?
Задача 25: Доказать, что существует число Фибоначчи, оканчивающееся на 0001.
Решение: Остатки чисел Фиббоначи по модулю 10\,000 образуют цикл.
Задача 26: Доказать, что существует число Фибоначчи, оканчивающееся на 9999.
Решение: «Минус первое» число Фиббоначи равно – 1. Задача 27: Доказать, что из 10 двузначных чисел можно выбрать две непересекающиеся группы с одинаковой суммой.
Решение: Всего наборов из 10 чисел больше 1000, сумма чисел в наборе может принимать менее тысячи значений. Значит модно найти два набора с одинаковой суммой. Эти наборы могут пересекаться, непересекающиеся наборы можно получить удалением из обоих наборов гирь, которые есть и там и там.
Задача 28: В каждой клетке доски 5 × 5 сидело по жуку. В некоторый момент каждый из них переполз на соседнюю (через сторону) клетку. Доказать, что какая-то клетка оказалась свободной.
Решение: Раскрасьте клетки в шахматном порядке.
Задача 29: Имеется n + 1 чисел из интервала от 1 до 2n – 1. Доказать, что среди них есть число, равное сумме двух других из них.
Решение: Подсказка: это максимальное число набора. Задача 30: Доказать, что среди 11 бесконечных десятичных дробей найдутся две, совпадающие в бесконечном числе разрядов.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Принцип Дирихле | Убрать решения |