 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Игры | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Игры |
|
|
Задача 2: a) В ряд лежат 25 монет. За ход разрешается брать одну или две рядом лежащие монеты. Проигрывает тот, кому нечего брать.
b) То же для 30 монет.
Задача 3: На окружности стоят 100 точек. Двое по очереди соединяют пары точек отрезками, причем отрезки не должны пересекаться. Проигрывает тот, у кого нет хода.
Задача 4: В двух кучах лежат по 100 конфет. За ход можно взять любое количество конфет из одной кучи. Выигрывает взявший последнюю.
Задача 5: Та же задача. но в начале в одной куче лежит 100 конфет, а в другой – 200.
Задача 6: На поле h8 шахматной доски стоит ладья. За ход можно передвинуть ее вниз или влево. Проигрывает тот, кому некуда ходить.
Решение: Выигрывает второй. Каждым своим ходом он должен возвращать ладью на диагональ. Задача 7: Та же задача, но ладья в начале стоит на поле e8.
Задача 8: Имеется доска 8 × 8. За ход можно положить доминошку на какие-то два ее поля (доминошки не должны перекрываться). Проигрывает тот, у кого нет хода.
Задача 9: Двое по очереди ставят коней на шахматную доску так, чтобы они не били друг друга. Проигрывает тот, у кого нет хода.
Задача 10: Двое по очереди ставят слонов на шахматную доску так, чтобы они не били друг друга. Проигрывает тот, у кого нет хода.
Задача 11: Та же задача для королей на доске 9 × 9.
Задача 12: (Игра «ЩЕЛК») Есть доска 50 × 50. Двое по очереди выбирают клетку и убирают («съедают») все клетки над ней и справа. Проигрывает «съевший» левую нижнюю клетку. Кто выигрывает?
Решение: Выигрывает первый. Первым ходом он должен «съесть» квадрат 49 × 49, а потом ходить симметрично.
Задача 13: Двое по очереди ставят крестики и нолики на доске 11 × 11. В конце игры для каждого столбца считают, каких в нем знаков больше: крестиков или ноликов. У кого столбцов с преобладанием его знака больше, тот и выиграл.
Задача 14: Двое по очереди ломают шоколадку размером 10 × 15 долек. За ход можно разломить любой имеющийся кусок вдоль линии. Проигрывает тот, кто первым получит дольку 1 × 1.
Задача 15: Двое по очереди ломают шоколадку размером 10 × 15 долек. За ход можно разломить любой имеющийся кусок вдоль линии. Выигрывает тот, кто первым получит дольку 1 × 1.
Задача 16: На столе лежат 15 спичек. За ход можно взять одну или две из них. Выигрывает взявший последнюю.
Задача 17: Имеется 40 конфет. Двое по очереди едят от одной до шести из них. Выигрывает съевший последнюю.
Задача 18: На одном конце полосы 3 × 103 стоит черная, на другом – белая шашка. Двое по очереди двигают каждый свою шашку на 1, 2, 3 или 4 клетки в направлении шашки соперника (перескакивать через чужую шашку запрещается). Проигрывает тот, кто не может сделать хода.
Задача 19: На одном конце полосы 3 × 103 стоит черная, на другом – белая шашка. Двое по очереди двигают каждый свою шашку на 1, 2, 3 или 4 клетки в любом направлении. (перескакивать через чужую шашку запрещается). Проигрывает тот, кто не может сделать хода. Решение: Выигрывает первый. Позиция проигрышна, если число клеток между шашками делится на 5. Задача 20: Игра начинается с числа 0. За ход можно прибавлять к имеющемуся числу любое число от 1 до 10. Выигрывает получивший число 100.
Задача 21: Игра начинается с числа 100. За ход разрешается уменьшить имеющееся число на любой из его делителей. Проигрывает тот, кто получит ноль.
Задача 22: В коробке лежат 300 спичек. За ход можно взять из коробка не более половины имеющихся в нем спичек. Проигрывает тот, кто не может сделать ход.
Решение: Выигрывает первый. В проигрышных позициях число спичек равно 2n – 1.
Задача 23: Имеется две кучи конфет: в первой – 40, во второй – 45. За ход нужно одну кучу съесть, а другую разделить на две (не обязательно равные). Проигрывает тот, кто не может сделать ход.
Решение: Выигрывает первый. Выигрышны те позиции, в которых хотя бы одна из кучек чётна. Задача 24: Какие поля выигрышные, а какие проигрышные на доске 8 × 8 в следующей игре: двое ходят по очереди королем влево, вниз или по диагонали влево-вниз. Проигрывает тот, у кого нет хода.
Задача 25: Какие поля выигрышные, а какие проигрышные на доске 8 × 8 в следующей игре: двое ходят по очереди ферзем влево, вниз или по диагонали влево-вниз. Проигрывает тот, у кого нет хода.
Решение:

Задача 26: В одной куче лежат 8 конфет, в другой – 4. Двое по очереди берут любое количество конфет из одной кучи или поровну из обеих. Выигрывает взявший последнюю конфету. Решение: Сравните с предыдущей задачей Задача 27: В одном коробке лежат 100 спичек, в другом – 200. За ход разрешается взять одну спичку из любого коробка, или по одной из каждого, или переложить спичку из одного в другой. Проигрывает тот, кто не может сделать хода.
Задача 28: Имеется две кучки по 11 спичек. За ход нужно взять две спички из одной кучки и одну из другой. Проигрывает тот, кто не может сделать хода.
Задача 29: Игра начинается с числа 1. За ход можно умножить имеющееся число на любое натуральное число от 2 до 9. Выигрывает тот, кто первым получит число, большее 1000.
Решение: Выигрывает первый. Проигрышные позиции – числа от 4 до 6 и от 56 до 111. Задача 30: В начале игры имеется куча из 11 камней. Двое по очереди берут один или два камня. Выигрывает, тот у кого в конце будет набрано четное число камней.
Задача 31: В начале игры имеется куча из 27 камней. Двое по очереди берут из нее от одного до четырех. Выигрывает тот, у кого в конце останется четное число камней.
Задача 32: На доске написано число 2. Двое игроков по очереди прибавляют к написанному числу некоторый его делитель (не равный самому числу). Проигрывает тот, кто первым напишет число a) большее 1989 b) большее 1990.
Решение: Выигрывает первый. а) Чётные числа выигрышны, а нечётные – проигрышны. b) Разберите два случая: выигрышно или проигрышно число 6. В обоих число 4 получается выигрышным.
Задача 33: Двое по очереди ломают шоколадку 5 × 10. За ход можно разломить один из имеющихся кусков на два вдоль углубления. Проигрывает тот, у кого нет хода.
Задача 34: На доске в ряд выписаны числа от 1 до 9. Двое по очереди ставят между ними плюсы и минусы. Когда все места заполнены, подсчитывается результат. Если он четен, выигрывает первый, а если нечетен – второй.
Задача 35: Двое по очереди ставят ладьи на шахматную доску так, чтобы они не били друг друга. Проигрывает тот, кто не может сделать хода.
Задача 36: На доске написаны числа 63 и 55. За ход разрешается дописать еще одно натуральное число – разность двух уже имеющихся. Числа на доске не должны повторяться. Проигрывает тот, у кого нет хода.
Решение: Выигрывает первый. Независимо от ходов соперников в конце будут выписаны все числа от 1 до 63. Задача 37: Двое играют в крестики-нолики на поле
 .
.Выигрывает поставивший три своих знака в ряд. Кто выигрывает при правильной игре?
Задача 38: На доске 3 × 10 стоят белая ладья и черный слон, которые ходят по очереди по шахматным правилам. Доказать, что ладья может взять слона.
Задача 39: Двое играют в шахматы, делая по очереди по два хода по обычным правилам. Доказать, что у второго игрока нет выигрышной стратегии.
Решение: Если бы у второго была выигрышная стратегия, то первый мог бы сделать «ход на месте», а затем использовать её для себя. Задача 40: Доказать, что в игре в крестики-нолики у второго игрока не может быть выигрышной стратегии независимо от размеров доски и того, сколько своих знаков нужно поставить в ряд для выигрыша.
Задача 41: В полосе 1 × 1989 в трех левых клетках стоит по шашке. За ход можно сдвинуть любую шашку вправо, не перескакивая через другие. Проигрывает тот, кто не может сделать хода.
Задача 42: В n коробках лежат 2n конфет. Двое игроков по очереди берут по одной конфете. Если последние две конфеты лежат в разных коробках, выигрывает первый, иначе – второй.
Решение: Выигрывает второй. После его ходов непустых коробок должно оставаться по крайней мере вдвое меньше, чем конфет. Задача 43: Двое играют в крестики-нолики на бесконечной клетчатой плоскости. Первый своим ходом может поставить два крестика, а второй – один нолик. Доказать, что первый может поставить 100 крестиков в ряд.
Решение: Сначала нужно поставить 2¹ºº крестиков по вертикали. По крайней мере 299 из них не будут иметь ноликов на своих горизонталях, и рядом с ними можно ставить очередные крестики. После этого остаётся 298 свободных пар крестиков… Продолжая в том же духе, можно поставить 100 крестиков в ряд. Задача 44: Двое играют в крестики-нолики на бесконечной клетчатой плоскости. Каждый стремится поставить свой знак 5 раз подряд по вертикали или горизонтали. Доказать, что второй игрок может играть так, что никогда не проиграет.
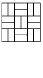
Решение: Разобьём плоскость на доминошки (см. рисунок) так, чтобы любая линия из 5 клеток содержала целую доминошку. Второй игрок на каждом ходу должен занимать вторую половину доминошки, в которую только что походил первый.
Решение: Выигрывает второй. Подсказка: 1001 делится на 77.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Игры | Убрать решения |