 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Комбинаторная геометрия | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Комбинаторная геометрия |
|
|
Задача 2: Доказать, что можно разрезать квадрат на: a) 6 b) 7 c) 8 квадратов d) любое число квадратов, большее 5.
Задача 3: Доказать, что n прямых общего положения разбивают плоскость на
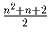 частей.
частей.Задача 4: Доказать, что куб можно разбить на любое число кубов, не меньшее 200.
Задача 5: Стороны выпуклого 100-угольника окрашены снаружи. Каждая диагональ окрашена с одной стороны. Доказать, что хотя бы один из кусков, на которые диагонали разбивают 100-угольник, будет окрашен лишь с внешней стороны.
Задача 6: На доске 8 × 8 отмечены центры всех клеток. Можно ли провести 13 прямых так, чтобы любые две отмеченные точки разделялись прямой?
Задача 7: Дано несколько отрезков на прямой. Любые два из них имеют общую точку. Доказать, что все они имеют общую точку.
Задача 8: Правильный 8-угольник разбит на параллелограммы. Доказать, что среди них есть a) по крайней мере один прямоугольник. b) по крайней мере два прямоугольника.
Задача 9: Плоскость раскрашена в два цвета. Доказать, что найдется
a) равносторонний треугольник
b) прямоугольник
с вершинами одного цвета.
Задача 10: На плоскости отмечено 100 красных и 100 синих точек. Доказать, что можно провести 100 непересекающихся отрезков, у каждого из которых один конец красный, а другой – синий. Задача 11:
Среди n прямых нет параллельных, и через любую точку пересечения двух из них проходит по крайней мере еще одна прямая. Доказать, что все прямые проходят через одну точку.
Задача 12:Даны несколько точек, не лежащих на одной прямой. Доказать, что найдется прямая, проходящая ровно через две данных точки.
Задача 13: Плоскость разбита на треугольники, причем их вершины не лежат на сторонах. Вершины раскрашены в 3 цвета так, что соседние вершины имеют разные цвета. Доказать, что треугольники можно раскрасить в два цвета так, чтобы соседние имели разные цвета.
Задача 14: На плоскости дано несколько точек (не меньше трех). Известно что для любых трех из этих точек найдется четвертая, образующая вместе с ними параллелограмм. Доказать, что точек всего четыре.
Задача 15: Доказать, что квадрат 8 × 8, из угла которого вырезан квадрат 1 × 1, нельзя разрезать на 17 равновеликих треугольников.
Задача 16: На плоскости нарисовано несколько непересекаюшихся кругов. Доказать, что есть круг, касающийся
a) не более шести кругов.
b) не более пяти кругов.
Задача 17: («Лемма Шпернера») Треугольник ABC разбит на треугольники, вершины которых не лежат на сторонах (но могут лежать на сторонах треугольника ABC). Вершины треугольников раскрашены в три цвета так, что на стороне AB (в том числе и на вершинах) нет цвета 1, на AC нет цвета 2, на BC нет цвета 3. Доказать, что найдется треугольник разбиения, все вершины которого имеют разные цвета.
Задача 18: В прямоугольнике 3 × 4 лежат 6 точек. Доказать, что есть 2 из них на расстоянии не больше
 .
.Задача 19: Доказать, что любой многоугольник можно диагоналями разбить на треугольники.
Задача 20: Доказать, что сумма углов (не обязательно выпуклого) n-угольника равна 180(n – 2).
Задача 21: Доказать, что на клетчатой бумаге нельзя нарисовать правильный треугольник с вершинами в узлах сетки.
Задача 22: (Формула Пика). Доказать, что площадь многоугольника с вершинами в узлах сетки равна
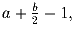 где a – число узлов внутри
многоугольника, b – число узлов на границе:
где a – число узлов внутри
многоугольника, b – число узлов на границе:a) для прямоугольника со сторонами, идущими по линиям сетки
b) для прямоугольного треугольника с катетами, идущими вдоль линий сетки
c) для многоугольника, составленного из двух других, для которых формула выполняется
d) для произвольного треугольника
e) для произвольного многоугольника.
Задача 23: Два многоугольника называются равносоставленными, если один из них можно разрезать на части, из которых можно сложить другой. Доказать, что
a) если A равносоставлен с B, а B равносоставлен с C, то A равносоставлен с C.
b) два равновеликих параллелограмма с общей стороной равносоставлены
c) два любых равновеликих параллелограмма равносоставлены
d) любой треугольник равносоставлен с некотрым параллелограммом
e) любой многоугольник равносоставлен с некоторым прямоугольником со стороной 1.
f) любые два многоугольника с одинаковой площадью равносоставлены.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Комбинаторная геометрия | Убрать решения |