 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Неравества | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Неравества |
|
|
Задача 2: Что больше: 215³³ или 5050?
215³³ < 5050, так как 50 > 7², а 215 < 7³.
Задача 3: Доказать, что у числа 2³ºº не меньше 90 и не больше 100 цифр.Задача 4: Доказать, что натуральное число не меньше: a) суммы b) произведения своих цифр.
Задача 5: Доказать, что
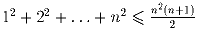 .
.Задача 6: Доказать, что
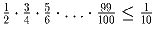 .
Решение:
Домножьте на большее число
.
Решение:
Домножьте на большее число
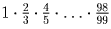 Задача 7:
Что больше a) 665 или 956?
Задача 7:
Что больше a) 665 или 956?b) 99! или 5099?
Задача 8: Доказать, что
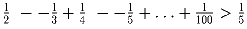 .
.Задача 9: Доказать, что в числе 3²ºº не более 100 цифр.
Задача 10: Доказать, что 2n > n при любом n.
Задача 11: Доказать, что 2n < n! при n ≥ 4.
Задача 12: Доказать, что n! ≤ nn.
Задача 13: x + y + z = 0. Доказать, что xy + yz + zx ≤ 0.
Задача 14: Доказать, что
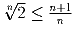 .
Задача 15:
Доказать:
.
Задача 15:
Доказать: 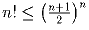 .
.Задача 16: Доказать неравенство Бернулли: (1 + x)n ≥ 1 + nx
a) если x > 0
b) если x > – 1.
Задача 17: a) Доказать, что
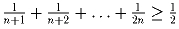 .
.
b) Существует ли n, для которого 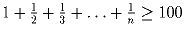 .
.
Задача 18: Доказать, что a)1,01¹ººº > 10.b)1,01¹ººº > 1000.
Задача 19: Доказать, что при любом положительном
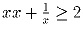 .
.Задача 20: x – положительное число, x(x + 1)(x + 2) … (x + 239) = 1. Доказать, что
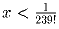 .
.Задача 21: Доказать, что
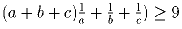 , если a,b,c > 0.
, если a,b,c > 0.Задача 22: a) a,b,c > 0. Доказать, что a² + b² + c² ≥ ab + bc + ac.
b) a,b,c – стороны треугольника. Доказать, что 2(ab + bc + ac) ≥ a² + b² + c².
Задача 23: a,b ≥ 0,a + b = 1. Доказать, что :
a) a² + b² ≥ ½.
b) a4 + b4 ≥ ⅛.
Задача 24: |x|,|y| < 1. Доказать, что
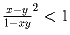 .
.Задача 25: Доказать, что
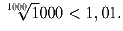
Задача 26: Что больше:
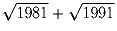 или
или 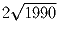 ?
Решение:
Правая часть больше
Задача 27:
a1, … ,an – положительные числа, произведение которых равно
единице. Доказать, что (1 + a1)(1 + a2) … (1 + an) ≥ 2n.
Решение:
При фиксированном ab величина (1 + a)(1 + b) тем меньше, чем
ближе числа a и b друг к другу. Сближая числа
a1, , an, можно сделать их всех равными единице.. Значение
левой части уменьшается, а в конце окажется равным 2n.
Задача 28:
Доказать, что
?
Решение:
Правая часть больше
Задача 27:
a1, … ,an – положительные числа, произведение которых равно
единице. Доказать, что (1 + a1)(1 + a2) … (1 + an) ≥ 2n.
Решение:
При фиксированном ab величина (1 + a)(1 + b) тем меньше, чем
ближе числа a и b друг к другу. Сближая числа
a1, , an, можно сделать их всех равными единице.. Значение
левой части уменьшается, а в конце окажется равным 2n.
Задача 28:
Доказать, что 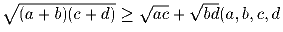 – положительные числа).
– положительные числа).Задача 29: Доказать, что
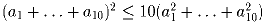 .
.Задача 30: Доказать, что
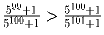 .
.Задача 31: Числа a и b таковы, что
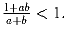 Доказать, что одно из
чисел a и b больше единицы, а другое меньше.
Доказать, что одно из
чисел a и b больше единицы, а другое меньше.Задача 32: a1,..,an > 0. Доказать, что
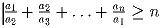 .
.Задача 33: x,y,z ≥ 0. Доказать, что
a) x³ + y³ + z³ ≥ 3xyz
b) x³ + y³ + z³ ≥ x²y + y²z + z²x ≥ 3xyz.
Задача 34: x ≥ y ≥ z ≥ t ≥ 0, x + y + z + t = 1. Доказать, что x² + 3y² + 5z² + 7t² ≤ 1.
Задача 35: a,b,c > 0. Доказать, что
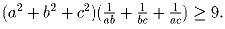
Задача 36: (Неравенство Чебышева) a) x1 > x2,y1 > y2. Доказать, что x1y1 + x2y2 > x1y2 + x2y1.
b) Даны два набора чисел x1, … ,xn и y1, … yn, причем xi перечислены в порядке возрастания. Числа yi переставляют всеми возможными способами и для каждой перестановки вычисляют выражение x1y1 + x2y2 + … + xnyn. Доказать, что наибольшее значение этого выражения достигается, когда yi переставлено в порядке возрастания, а наименьшее, когда они переставлены в порядке убывания.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Неравества | Убрать решения |