 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Остатки | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Остатки |
|
|
Задача 2: Число x оканчивается на 5. Доказать, что x² оканчивается на 25.
Задача 3: Найти последнюю цифру числа 71988 + 91988.
Задача 4: Доказать, что квадрат натурального числа не может оканчиваться на две нечетные цифры.
Задача 5: Найти последнюю цифру числа 1 • 2 + 2 • 3 + … + 999 • 1000.
Задача 6: На сколько нулей оканчивается число 9999 + 1? Решение: На один Задача 7: Найти наименьшее натуральное N, дающее остаток 1 по модулю 2, 2 по модулю 3, … ,7 по модулю 8. Решение: НОД (2,3,4 … ,8) – 1. Задача 8: Доказать, что если a² + b² делиться на 7, то и ab делится на 7.
Задача 9: Доказать, что 43²³ + 2343 делится на 66.
Задача 10: Доказать, что 4343 + 1717 делится на 10.
Задача 11: Найти остаток 1316 – 255 • 515 по модулю 3.
Задача 12: Доказать, что 776776 + 777777 + 778778 делится на 3.
Задача 13: Найти остаток 418 + 517 по модулю 3.
Задача 14: Найти остаток (116 + 1717)²¹ • 749 по модулю 8.
Решение: 3
Задача 15: Доказать, что для любого n a) 72n – 42n делится на 33
b) 36n – 26n делится на 35.
Задача 16: Доказать,что 1985!! + 1986!! делится на 1987.
Задача 17: Доказать, что для любого n
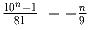 – целое число.
– целое число.Задача 18: Доказать, что при четном n 20n + 16n – 3n – 1 делится на 323. Решение: Подсказка: 323 = 17 • 19 Задача 19: Доказать, что (2n – 1)n – 3 делится на 2n – 3 при любом n.
Задача 20: Доказать, что n³ + 5n делится на 6 при любом n.
Задача 21: Доказать, что 22n – 1 + 3n + 4 делится на 9 при любом n.
Задача 22: x² ≡ y² (mod %)%239. Доказать, что x ≡ y или x ≡ – y.
Задача 23: Доказать, что
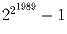 делится на 17.
делится на 17.Задача 24: a1 = a2 = 1, an + 1 = anan – 1 + 1. Доказать, что an не делится на 4.
Задача 25: Доказать, что
a) Степень двойки не может оканчиваться на 4 одинаковых цифры.
b) Квадрат не может состоять из одинаковых цифр (если он не однозначный).
c) Квадрат не может оканчиваться на 4 одинаковых цифры.
Задача 26: Доказать, что n-е простое число больше 3n при n > 12. Решение: Рассмотрите остатки по модулю 6. Задача 27: 2n = 10a + b, b < 10. Доказать, что ab делится на 6.
Задача 28: Доказать, что существует бесконечно много простых чисел вида 4k + 3.
Задача 29: В государстве имеют хождение монеты в один золотой и в один грош, причем один золотой составляет 1001 грошей. Можно ли, имея 1986 золотых, купить без сдачи несколько предметов по 1987 грошей?
Задача 30: n + 1 делится на 24. Доказать, что сумма делителей n делится на 24.
Решение: Докажите, что n – не квадрат и разбейте делители на пары.
Задача 31: a ≡ 68 (mod %)%1967, a ≡ 69 (mod %)%1968. Найти остаток a по модулю 14.
Задача 32: Доказать, что существует бесконечно много простых чисел вида 6k + 5.
Задача 33: Доказать, что 3n + 1 не делится на 10¹ºº. Решение: Оно не делится даже на 8.
Задача 34: p – простое число. Доказать, что остаток p по модулю 30 – простое число или 1. Задача 35: m и n взаимно просты, b – произвольное целое число. Доказать, что числа b, b + n, b + 2n, … ,b + (n – 1)n дают все возможные остатки по модулю m.
Задача 36: Найти a) 3 последние цифры b) 6 последних цифр числа 1999 + 2999 + … + (106 – 1)999.
Задача 37: Доказать, что a2n + 1 + (a – 1)n + 2 делится на a² – a + 1.
Задача 38: p и q – простые числа больше 3. Доказать, что p² – q² делится на 24.
Задача 39: Может ли m! + n! оканчиваться на 1990?
Задача 40: Доказать, что n² + 5n + 16 не делится на 169 ни при каком натуральном n. Решение: n² + 5n + 16 = (n – 4)² + 13n. Задача 41: При каких n n² – 6n – 4 делится на 13?
Задача 42: Доказать, что в любой бесконечной арифметической прогрессии
a) Имеется бесконечно много составных чисел.
b) Имеется или бесконечно много квадратов, или ни одного.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Остатки | Убрать решения |