 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Преобразование алгебраических выражений. | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Преобразование алгебраических выражений. |
|
|
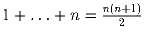
Задача 2: Найти: a) 2 + 4 + 6 + … + 2n.
b) 1 + 3 + 5 + … + (2n – 1).
Задача 3: Доказать тождества:
a) an – bn = (a – b)(an – 1 + an – 2b + an – 3b² + … + bn – 1)
b) an + bn = (a + b)(an – 1 – an – 2b + an – 3b² + … + bn – 1) при нечетном n.
Задача 4: a) Доказать, что nk – 1 делится на n – 1
b)Доказать,что ak – bk делится на a – b.
c) При каких k nk + 1 делится на n + 1 для любого n?
d) При каких k ak + bk делится на a + b для любых a и b?
Задача 5: a0, … ,an – арифметическая прогрессия с разностью d. Доказать, что a)
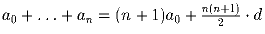
b) 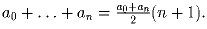
Задача 6: Доказать, что 1 + 2 + 4 + … + 2k – 1 = 2k – 1.
Задача 7: Доказать:
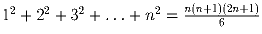 .
.Задача 8: Доказать, что
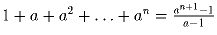 .
.Задача 9: Найти 1 + 11 + 111 + … + 11 … 1 (в последнем слагаемом n единиц). Задача 10: Найти
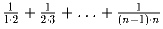 .
.Задача 11: Найти 1 • 1! + 2 • 2! + … + n • n!.
Задача 12: Вещественное число x таково, что
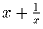 – целое. Доказать, что
при любом
– целое. Доказать, что
при любом 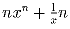 – целое.
Решение:
– целое.
Решение: ПО индукции с помощью тождества
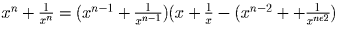
Задача 13:
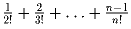 .
.Задача 14: Разложить на множители:
a) a² + b² – (c² + 2ab),
b) a4 + 4b4.
Решение:b) (a² + 2b² + 2ab)(a² + 2b² – 2ab
Задача 15: Доказать, что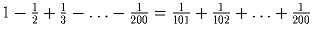 .
.Задача 16: Доказать, что
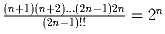 .
.Задача 17: Доказать, что a) 1030721 – составное число.
b) 28 + 25 • 56 + 5¹² – составное число.
Решение:а) Оно делится на 103
b) Оно равно (24 + 56)²
Задача 18: Доказать, что число a) 57599 b) 343001 – составное. Решение:
a) 24² – 1; b) 70³ + 1.
Задача 19: Доказать, чтоa)
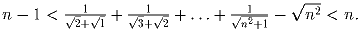
c) суммы в пунктах a) и b) равны.
Решение: Эти выражения равны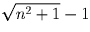 .
.Задача 20: a) Найти
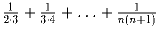 .
.b) Доказать, что 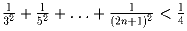 .
.
Задача 21: Найти
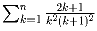 .
.22 a,b,c – целые числа, a + b + c = 0. Доказать, что 2(a4 + b4 + c4) – точный квадрат.
Задача 23: Целые числа a и b представляются в виде суммы двух квадратов целых чисел. Доказать, что их произведение тоже представляется в виде суммы квадратов.
Задача 24: Доказать, что число 2¹º + 5¹² – составное.
Задача 25: Доказать, что a) Если 2n – 1 – простое, то и n – простое.
b) Если 2n + 1 – простое, то n – степень двойки.
Задача 26: Разложить 258 + 1 на 3 множителя.
Задача 27: x1 = 2,xn + 1 – наибольший простой делитель числа x1x2 … xn + 1. Доказать, что xn не равно 5 при любом n.
Решение: x1 = 2, x2 = 3 и больше двоек и троек не встретится. xn + 1 может быть равно 5 только если x1x2 … xn не делится на 4.
Задача 28: Доказать, что число 11 … 122 … 2 (100 единиц и 100 двоек) является произведением двух последовательных натуральных чисел.
Задача 29:
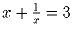 . Найти: a)
. Найти: a) 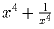 b)
b)
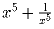 .
.Задача 30: Доказать, что число 11 … 155 … 56(100 единиц, 99 пятерок) является точным квадратом.
Задача 31:
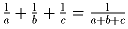 .
Доказать, что среди чисел a, b и c есть
два с суммой, равной нулю.
.
Доказать, что среди чисел a, b и c есть
два с суммой, равной нулю.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Преобразование алгебраических выражений. | Убрать решения |