 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Задачи на прямоугольных досках | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Задачи на прямоугольных досках |
|
|
b) То же для 44 ферзей.
Задача 2: Какое максимальное число не бьющих друг друга a) ладей. b) королей можно расставить на доске 8 × 8?
a) 8. На каждой вертикали стоит не больше одной ладьи. b) 16. В каждом квадрате 2 × 2 находится не больше одного короля.
Задача 3: Какое наибольшее число не бьющих друг друга a) слонов b)коней можно расставить на доске 8 × 8?
a) 14; b) 32
Задача 4: В таблице 10 × 10 расставлены числа, причем в любой фигуре
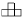 сумма чисел равна 4. Доказать, что все числа равны 1.
сумма чисел равна 4. Доказать, что все числа равны 1.Задача 5: Какое минимальное число клеток нужно закрасить в квадрате 6 × 6, чтобы из остатка нельзя было вырезать уголок вида
 .
.18. В каждом квадрате 2 × 2 необходимо закрасить две клетки.
Задача 6: В какое минимальное число цветов нужно покрасить клетки доски 8 × 8 так, чтобы любые две соседние (через сторону или вершину) клетки были разных цветов?Задача 7: На поле для морского боя размера 10 × 10 стоит корабль 1 × 4. Какое минимальное количество выстрелов нужно сделать, чтобы наверняка в него попасть?
Задача 8: На доске 8 × 8 стоят 20 ладей, которые бьют все поля. Доказать, что из них можно выбрать 8 ладей, которые бьют все поля.
Ладьи имеются или на всех вертикалях, или на всех горизонталях.
Задача 9: Какое минимальное количество королей нужно расставить на доске 12 × 12, чтобы они били все клетки?Задача 10: На доске 10 × 10 стоит 51 ладья. Доказать, что можно выбрать 6 ладей, не бьющих друг друга.
Докажите по индукции общее утверждение: из nk + 1 ладей на доске n × n можно выбрать k + 1 небьющих друг друга. Указание: выберите ладью, которая бьёт не больше n + k – 2 других.
Задача 11: Можно ли раскрасить доску 6 × 6 в 6 цветов так, чтобы в любом прямоугольнике 2 × 3 были все 6 цветов?Задача 12: Расставить на доске 8 × 8 наибольшее число королей так, чтобы каждая клетка билась не более одного раза.
Задача 13: Какое минимальное число королей надо расставить на доске a) 4 × 4 b)10 × 10 так, чтобы они били все клетки?
a) 4; b) 16. Каждый король может бить только одну из отмеченных на рисунке клеток.

Задача 14: В квадрате 3 × 3 закрашено 5 клеток. Доказать, что найдется закрашенная клетка, в строке и в столбце которой найдется еще по одной закрашенной клетке.
Задача 15: Из квадрата 30 × 30 вырезали 99 квадратов 2 × 2 (по линиям сетки). Доказать, что можно вырезать еще один. Решение: Если это не так, то квадраты 3 × 3 с теми же центрами, что и вырезанные 2 × 2, покрывают квадрат 29 × 29, что невозможно.
Задача 16: В квадрате 6 × 6 расставлены числа от 1 до 36. Может ли при этом сумма чисел в любой фигуре вида
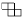 делиться на 9?
делиться на 9?Задача 17: Доска 8 × 8 раскрашена в два цвета. Доказать, что клетки одного из цветов можно обойти ферзем (не останавливаясь на клетках другого цвета).
Задача 18: В некоторых клетках доски m × n стоят фишки. Каждая фишка единственная в своем столбце или в своей строке. Каково максимально возможное число фишек?
Решение: m + n – 1. Доказывайте это по индукции.
Задача 19: На доске n × n стоят несколько ладей так, что в любом кресте, составленном из вертикали и горизонтали, центральная клетка которого пуста, стоят ровно n ладей. Доказать, что ладей не меньше
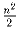 .
Решение:
Пусть k – количество ладей в одной из строк. Можно считать, что
.
Решение:
Пусть k – количество ладей в одной из строк. Можно считать, что
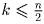 . Пучть имеется l строк с k ладьями и m столбцов
с n – k ладьями. Можно считать, что это нижние l строк и правые m
столбцов. Легко видеть, что m ≥ n – k и l ≥ k. Кроме того, левый
нижний прямоугольник l × (n – m) целиком заполнен ладьями (иначе
найдутся ещё столбцы с n – k ладьями. Значит всего ладей не меньше чем
. Пучть имеется l строк с k ладьями и m столбцов
с n – k ладьями. Можно считать, что это нижние l строк и правые m
столбцов. Легко видеть, что m ≥ n – k и l ≥ k. Кроме того, левый
нижний прямоугольник l × (n – m) целиком заполнен ладьями (иначе
найдутся ещё столбцы с n – k ладьями. Значит всего ладей не меньше чем
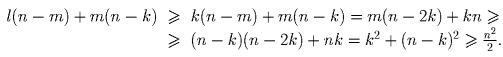
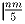 .
Решение:
Используйте следующий план решения. Во-первых, на краю прямоугольника не
может быть свободных клеток. Во-вторых, четыре клетки, соседние (через
сторону) с одной свободной, должны быть заняты. В-третьих, у разных
свободных клеток наборы соседей не пересекаются.
.
Решение:
Используйте следующий план решения. Во-первых, на краю прямоугольника не
может быть свободных клеток. Во-вторых, четыре клетки, соседние (через
сторону) с одной свободной, должны быть заняты. В-третьих, у разных
свободных клеток наборы соседей не пересекаются.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Задачи на прямоугольных досках | Убрать решения |