 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Задачи с цифрами | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Задачи с цифрами |
|
|
Задача 2: ab + ba = x². Найти x.
Задача 3: Доказать, что сумма всех девяти двузначных чисел, составленных из трех данных цифр, делится на 11.
Задача 4: Доказать, что abc – cba делится на 99.
Задача 5: а, б, в, г, д, е – различные цифры. Доказать,что:
a) 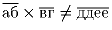
б) 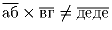 в)
в) 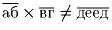
Задача 7: Доказать, что
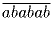 делится на 21.
делится на 21.Задача 8: Может ли квадрат в десятичной записи состоять из
a) 601 шестерок и нескольких нулей?
b) 606 шестерок и нескольких нулей?
Задача 9:
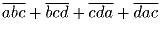 делится на 9.
Доказать, что
делится на 9.
Доказать, что 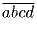 делится на 3.
делится на 3.Задача 10: a) Найти все числа
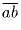 , равные 9(a + b).
, равные 9(a + b).
b) найти все числа 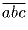 , равные 18(a + b + c).
, равные 18(a + b + c).
Задача 11: Сумма цифр числа A равна сумме цифр 2A. Доказать, что A делится на 9.
Задача 12: Найти сумму всех шестизначных чисел, составленных из цифр 1, 2 и 3. Решение: 222222 • 36 Задача 13: Число n записано 4k единицами и k двойками. Доказать, что k + 6 – составное.
Задача 14: Верно ли что если сумма цифр числа делится на 27, то и само число делится на 27? Решение: Нет. Наименьший контрпример – 1899 Задача 15: Автобусный билет – это бумажка с написанным на ней 6-значным числом (возможно, начинающееся нулями). Билет называется счастливым, если сумма первых трех его цифр равна сумме остальных.
a) Четно или нечетно число счастливых билетов?
b) Доказать, что сумма номеров счастливых билетов делится на 13.
c) Каких номеров больше: счастливых или кратных 11?
Задача 16: Калькулятор при нажатии кнопки делает из числа его сумму цифр.
a) Доказать, что из любого числа от 1 до 106 через три нажатия получится цифра.
b) Каких цифр получится больше единиц или пятерок? (из тех же чисел от 1 до 106).
Задача 17: Найти все наборы различных цифр a,b,c,такие что
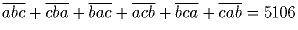 .
.Задача 18: Доказать, что число 111 … 1 (44 единицы) кратно 121.
Задача 19: a) Доказать,что
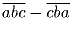 – не квадрат
– не квадрат
b) Может ли 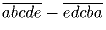 быть квадратом?
быть квадратом?
Задача 20: Цифры числа N переставили, и оно уменьшилось в 3 раза. Доказать, что N делится на 27.
Задача 21: x² + 1 – десятизначное число. Доказать, что в нем есть две одинаковые цифры.
Задача 22: Число состоит из 10 шестерок, 30 пятерок и 60 двоек. Доказать, что оно – не квадрат.
Задача 23: Доказать признак делимости на 11:
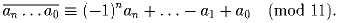
Задача 24: N делится на 99. Доказать, что сумма цифр N не меньше 18. Решение: Используйте признаки делимости на 9 и 11.
Задача 25: Доказать, что среди любых 18 последовательных трехзначных чисел найдется число, делящееся на свою сумму цифр.
Задача 26: Доказать, что
a) 11 … 1 (3n единиц) делится на 33 … 3 (n троек)
b) Число из 3n троек делится на 3n.
Задача 27:
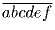 делится на 37. Доказать, что
делится на 37. Доказать, что 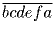 делится на 37.
делится на 37.Задача 28:
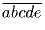 делится на 41. Доказать,
что
делится на 41. Доказать,
что 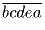 делится на 41.
делится на 41.Задача 29: Доказать, что
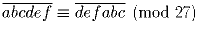 .
.Задача 30: Из числа вычитают его сумму цифр. Доказать, что после 100 таких операций из трехзначного числа получится ноль.
Задача 31: Числа 1,2,3, … ,1991 выписаны друг за другом в произвольном порядке. Доказать, что полученное число не является кубом.
Задача 32: a) Написано 19, затем k нулей, затем 80. При каких k это число делится на 1980?
b) В ряд выписаны числа от 19 до 80. Доказать, что полученное число делится на 1980.
Решение: Подсказка: 1980 = 9 • 11 • 20 Задача 33: Сколько есть 1990-значных чисел, любая перестановка цифр которых делится на 7? Решение: Такие числа состоят только из семёрок и нулей. Ответ: 21989Задача 34: Что больше: сумма цифр всех 10-значных чисел или сумма цифр всех 11-значных чисел, делящихся на 5?
Задача 35: Доказать, что существует натуральное число, делящееся на 5¹ºº, 100 последних цифр которого не равны нулю. Решение: Будем по индукции строить число из k ненулевых цифр, делящееся на 5k. Если такое (k – 1)-значное число уже построено и делится на 5k, припишем в его начало пятёрку. Если же оно не делится на 5k, то можно приписать цифру, которая компенсирует его остаток.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Задачи с цифрами | Убрать решения |