 |
 |
|
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Замощения | Убрать решения |
|
|
| Математический кружок. Задачник первого-второго года обучения. Замощения |
|
|
Задача 2: Из шахматной доски 8 × 8 вырезаны противоположные угловые клетки. Можно ли остаток разрезать на прямоугольники 1 × 2 (доминошки)? Решение: Нет. Каждая доминошка занимает одну чёрную и одну белую клетки, а на доске без углов чёрных и белых клеток разное число.
Задача 3: Из противоположных углов доски 10 × 10 вырезаны два квадрата 3 × 3. Можно ли остаток разрезать на доминошки?
Задача 4: Придумать связную фигуру на шахматной доске, в которой поровну черных и белых клеток, но которую нельзя разбить на доминошки.
Задача 5: Можно ли разрезать квадрат 10 × 10 на 25 фигур
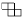 ?
?Задача 6: Можно ли разрезать квадрат 10 × 10 на 25 фигур
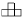 ?
Решение:
Раскрасьте доску в шахматном порядке. Чёрных клеток окажется чётное
число, а в каждую фигурку их попадёт одна или три.
Задача 7:
Можно ли разрезать квадрат 10 × 10 на 25 фигур
?
Решение:
Раскрасьте доску в шахматном порядке. Чёрных клеток окажется чётное
число, а в каждую фигурку их попадёт одна или три.
Задача 7:
Можно ли разрезать квадрат 10 × 10 на 25 фигур
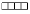 ?
Решение:
?
Решение: Раскрасьте доску в четыре цвета (см. рисунок). Каждая фигурка занимает по одной клетке каждого цвета, а клеток первого и второго цвета разное число.
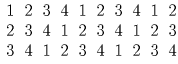
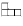 ?
Решение:
Покрасьте вертикаличерез одну.
Задача 9:
Доказать, что доску 8 × 8 без угловой клетки нельзя разрезать на
прямоугольники 1 × 3.
?
Решение:
Покрасьте вертикаличерез одну.
Задача 9:
Доказать, что доску 8 × 8 без угловой клетки нельзя разрезать на
прямоугольники 1 × 3.Задача 10: Можно ли доску 8 × 8 разрезать на один квадрат 2 × 2 и 15 фигур вида
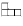 ?
?Задача 11: Квадрат a)5 × 5b)8 × 8 разбили на несколько прямоугольников 3 × 1 и один квадрат 1 × 1. Где может стоять квадрат 1 × 1? Решение: а) В центре, b) На третьей клетке по диагонали от любого угла.
Указание: раскрасьте доску в три цвета.
Задача 12: Какое максимальное количество брусков 1 × 1 × 4 можно вырезать из куба 6 × 6 × 6?Задача 13: Прямоугольник разбит на фигурки
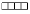 и
и  .
Одну из
.
Одну из 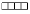 потеряли, но заменили ее на
потеряли, но заменили ее на  .
Доказать, что новым набором
покрыть исходный прямоугольник нельзя.
.
Доказать, что новым набором
покрыть исходный прямоугольник нельзя.Задача 14: Можно ли квадрат 16 × 16 разбить на 64 прямоугольника 1 × 4, из которых 31 будут стоять вертикально, а остальные 33 – горизонтально? Решение: Покрасьте каждую четвёртую вертикаль. Задача 15: При каких n квадрат n × n можно разбить на a)
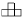 ;
;b)
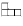 ?
?
a) при n = 3
b) при n = 4
c) для любого n.
Решение:Раскрасьте в n цветов.
Задача 17: Доказать, что прямоугольник m × n можно разбить на прямоугольники a × b, тогда и только тогда, когда выполняются следующие условия:
1) m и n представляются в виде ka + lb (k и l – целые неотрицательные числа)
2) m и n делится на a.
3) m или n делится на b.
Задача 18: Прямоугольник m × n называется прочным, если его можно разбить на доминошки так, что любой разрез прямоугольника пересекает хотя бы одну доминошку. Доказать, что:
a) прямоугольник 2 × n – непрочный
b) прямоугольник 3 × n – непрочный
c) прямоугольник 4 × n – непрочный
d) прямоугольники 5 × 6 и 6 × 8 – прочные
e) если прямоугольник m × n – прочный, то и прямоугольник m × (n + 2) – прочный.
f)* прямоугольник 6 × 6 – непрочный
g) Какие прямоугольники являются прочными, а какие нет?
Решение: f) Подсказка: каждая линия в квадрате 6 × 6 пересекает чётное число доминошек.
g) Все прямоугольники m × n, где mn чётно, m,n ≥ 5, кроме 6 × 6.
Задача 19:Уголком называется фигура вида
 .
.
a) Можно ли прямоугольник 5 × 9 разбить на уголки?
b) Доказать, что прямоугольник со сторонами,большими 100 и площадью, делящейся на 3, можно разбить на уголки.
c) Какие прямоугольники можно разбить на уголки, а какие – нет?
Задача 20:
Можно ли доску 2n × 2n без угловой клетки разбить на уголки?
Решение: Да, можно. Разбиение строится по индукции. Задача 21: При каких n доску (2n + 1) × (2n + 1) без угловой клетки можно разбить на доминошки, среди которых поровну вертикальных и горизонтальных?Решение: При чётных n.
| Задачная база >> Разное >> Задачник первого-второго года обучения >> Замощения | Убрать решения |