 |
 |
|
| Задачная база >> Разное >> Математический кружок. 1-й год >> Делимость и остатки >> Алгоритм Евклида | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок. Делимость и остатки. Алгоритм Евклида |
|
|
Найти наибольший общий делитель чисел 2n + 13 и n + 7.
Решение:НОД (2n + 13,n + 7) = НОД (n + 7,n + 6) = НОД (n + 6,1) = 1.
Задача 55:
Докажите, что дробь 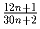 –
несократима ни при каком натуральном n.
–
несократима ни при каком натуральном n.
Решение:
НОД (30n + 2,12n + 1) = НОД (12n + 1,6n) = НОД (6n,1) = 1.
Задача 56:Найдите НОД (2¹ºº – 1,2¹²º – 1).
Решение:Указание: Воспользуйтесь алгоритмом Евклида.
Задача 57:
Найдите НОД (111 … 111,11 … 11) – в записи первого числа 100 единиц, в записи второго – 60.
Решение:
Указание: Воспользуйтесь алгоритмом Евклида.
| Задачная база >> Разное >> Математический кружок. 1-й год >> Делимость и остатки >> Алгоритм Евклида | Убрать решения |