 |
 |
|
| Задачная база >> Разное >> Математический кружок. 1-й год >> Делимость и остатки >> Несколько задач | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок. Делимость и остатки. Несколько задач |
|
|
а) a + 1 делится на 3. Докажите, что 4 + 7a делится на 3.
б) 2 + a и 35 – b делятся на 11. Докажите, что a + b делится на 11.
Решение:Указания: а) 4 + 7a = 4(a + 1) + 3a; б) a + b = (2 + a) – (35 – b) + 33.
Задача 47:
Найдите последнюю цифру числа 1² + 2² + … + 99².
Решение:
0
Задача 48:
Про семь натуральных чисел известно, что сумма любых шести из них делится на 5. Докажите, что каждое из данных чисел делится на 5.
Решение:
Докажите, что любые два числа из этих семи дают одинаковый остаток от деления на 5. Для этого рассмотрите две шестерки: одну – не содержащую первое из них, вторую – не содержащую второе.
Задача 49:Докажите, что сумма n последовательных нечетных натуральных чисел при n > 1 является составным числом.
Решение:
Обозначим первое из этих чисел через a. Получим
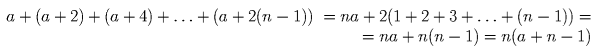
Найдите наименьшее число, дающее следующие остатки: 1 – при делении на 2, 2 – при делении на 3, 3 – при делении на 4, 4 – при делении на 5, 5 – при делении на 6.
Решение:
Заметим, что это число, увеличенное на 1, делится на 2, 3, 4, 5, 6. Ответ: 59.
Задача 51:Докажите, что если (n – 1)! + 1 делится на n, то n – простое число.
Решение:Если n – составное число (n > 4), то (n – 1)! делится на n.
Задача 52:Докажите, что существует такое натуральное n, что числа n + 1, n + 2, …, n + 1989 – составные.
Решение:
Попробуем рассказать, как можно придти к решению. Число n + 1 должно быть составным. Попытаемся пойти по самому простому пути: сделаем так, чтобы n + 1 делилось на 2. n + 2 также должно быть составным, но делиться на 2 уже не может. Попытаемся опять пойти по самому простому пути: хотелось бы сделать так, чтобы n + 2 делилось на 3. Продолжая в том же духе, можно пытаться найти число n такое, что n + 1 делится на 2, n + 2 – на 3, n + 3 – на 4 и так далее. Это равносильно тому, что n – 1 делится на 2, 3, 4, …, 1990. Такое число, конечно, существует – например, 1990!. Итак, в качестве искомого n можно взять число 1990! + 1.
Задача 53:
Докажите, что существует бесконечно много простых чисел.
Решение:
Предположим противное. Пусть p1, p2, …, pn – все простые числа. Рассмотрим число p1p2 … pn + 1. Это число не делится ни на одно из чисел p1, p2, …, pn и, следовательно, не может быть разложено в произведение простых. Противоречие.
| Задачная база >> Разное >> Математический кружок. 1-й год >> Делимость и остатки >> Несколько задач | Убрать решения |