 |
 |
|
| Задачная база >> Разное >> Математический кружок. 1-й год >> Нулевой цикл | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок. Нулевой цикл |
|
|
В стакане находятся бактерии. Через секунду каждая из бактерий делится пополам, затем каждая из получившихся бактерий через секунду делится пополам и так далее. Через минуту стакан полон. Через какое время стакан был заполнен наполовину?
Решение:
Ответ: Через 59 секунд.
Задача 2:Аня, Ваня и Саня сели в автобус, не имея медных монет, однако сумели заплатить за проезд, потратив по пять копеек каждый. Как им это удалось?
Решение:
Аня и Ваня платят Сане 15 копеек, получая от него по 10 копеек сдачи. После этого он платит 15 копеек в кассу.
Задача 3:Из книги выпал кусок, первая страница которого имеет номер 328, а номер последней записывается теми же цифрами в каком-то другом порядке. Сколько страниц в выпавшем куске?
Решение:
Ответ: 495 страниц.
Задача 4:В мешке 24 кг гвоздей. Как, имея только весы без стрелки, отмерить 9 кг гвоздей?
Решение:
Разбиваем сначала гвозди пополам – на две группы по 12 кг, после чего одну из этих групп делим пополам, а затем еще раз пополам. Полученные 3 кг гвоздей откладываем и получаем 9 кг в остатке.
Задача 5:Червяк ползет по столбу, начав путь от его основания. Каждый день он проползает вверх на 5 см, а за каждую ночь сползает вниз на 4 см. Когда он достигнет верхушки столба, если его высота равна 75 см?
Решение:
Ответ: Червяк окажется вверху к вечеру 71-го дня.
Задача 6:В январе некоторого года было четыре пятницы и четыре понедельника. Каким днем недели было 20-е число этого месяца?
Решение:
Ответ: Воскресенье.
Задача 7:Сколько клеток пересекает диагональ в клетчатом прямоугольнике размерами 199 × 991?
Решение:
Ответ: Диагональ пересекает 199 + 991 – 1 = 1189 клеток.
Задача 8:Из числа 1234512345123451234512345 вычеркните 10 цифр так, чтобы оставшееся число было максимально возможным.
Решение:
Ответ: Максимальное число это 553451234512345.
Задача 9:Петя говорит: позавчера мне еще было 10 лет, а в следующем году мне исполнится 13. Может ли такое быть?
Решение:
Ответ: Да, может, если день рождения Пети – 31 декабря, а указанную фразу он произносит 1 января.
Задача 10:Петин кот перед дождем всегда чихает. Сегодня он чихнул. «Значит, будет дождь» – думает Петя. Прав ли он?
Решение:
Ответ: Нет, не прав.
Задача 11:Учитель рисует на листке бумаги несколько кружков и спрашивает одного ученика: «Сколько здесь кружков?». «Семь»– отвечает ученик. «Правильно. Так сколько здесь кружков?» – опять спрашивает учитель другого ученика. «Пять» – отвечает тот. «Правильно» – снова говорит учитель. Так сколько же кружков он нарисовал на листке?
Решение:
Ответ: Всего нарисовано 12 кружков: пять на одной стороне листка и семь – на другой.
Задача 12:Сын отца профессора разговаривает с отцом сына профессора, причем сам профессор в разговоре не участвует. Может ли такое быть?
Решение:
Ответ: Да, может, если профессор – женщина.
Задача 13:По дороге цепочкой ползут три черепахи. «За мной ползут две черепахи» – говорит первая. «За мной ползет одна черепаха, и передо мной ползет одна черепаха» – говорит вторая. «Передо мной ползут две черепахи, и за мной ползет одна черепаха» – говорит третья. Как такое может быть?
Решение:
Он рассуждал так: «Если у меня лицо не испачкано, то другой мудрец, увидев, что третий над чем-то смеется, понял бы, что его лицо испачкано, и перестал бы смеяться. Однако он смеется, следовательно, у меня лицо тоже испачкано.»
Задача 14:В поезде едут три мудреца. Внезапно поезд въезжает в туннель, и после того, как загорается свет, каждый из мудрецов видит, что лица его коллег испачканы сажей, влетевшей в окно вагона. Все трое начинают смеяться над своими испачкавшимися попутчиками, однако внезапно самый сообразительный мудрец догадывается, что его лицо тоже испачкано. Как ему это удалось?
Решение:
Он рассуждал так: «Если у меня лицо не испачкано, то другой мудрец, увидев, что третий над чем-то смеется, понял бы, что его лицо испачкано, и перестал бы смеяться. Однако он смеется, следовательно, у меня лицо тоже испачкано.»
Задача 15:Из стакана молока три ложки содержимого переливают в стакан с чаем и тщательно размешивают смесь. Затем три ложки смеси переливают обратно в стакан с молоком. Чего теперь больше: чая в стакане с молоком или молока в стакане с чаем?
Решение:
Ответ: Конечно же, чая в молоке столько же, сколько молока в чае.
Задача 16:Составьте из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 магический квадрат, то есть разместите их в таблице 3 × 3 так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы.
Решение:

Задача 17:
В примере на сложение цифры заменили буквами (причем одинаковые цифры – одинаковыми буквами, а разные цифры – разными буквами) и получили: БУЛОК + БЫЛО = МНОГО. Сколько же было булок? Их количество есть максимальное возможное значение числа МНОГО.
Решение:
Ответ: 95343
Задача 18:
Разведка звездной империи ФИГ-45 перехватила секретное шифрованное сообщение враждебной планеты Медуза: ДУРАК + УДАР = ДРАКА. Известно, что разные цифры зашифрованы разными буквами, а одинаковые цифры – одинаковыми буквами. Два электронных думателя взялись найти решение и получили два разных ответа. Может ли такое быть или один из них надо сдать в переплавку?
Решение:
Ответ: Нет. Решение лишь одно: 51286 + 1582 = 52868.
Задача 19:Как разложить по семи кошелькам 127 рублевых бумажек так, чтобы любую сумму от 1 до 127 рублей можно было бы выдать, не открывая кошельков?
Решение:
127 бумажек надо разложить так: 1 + 2 + 4 + 8 + 16 + 32 + 64.
Задача 20:
Разрежьте уголок, изображенный на рисунке на четыре таких же уголка вдвое меньшего размера.

Решение:
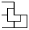
Задача 23:
Можно ли расположить 6 длинных круглых карандашей так, чтобы каждый из них касался любого другого?
Задача 24:При помощи ножниц вырежьте в тетрадном листе дырку, через которую мог бы пролезть слон!
| Задачная база >> Разное >> Математический кружок. 1-й год >> Нулевой цикл | Убрать решения |