 |
 |
|
| Задачная база >> Разное >> Математический кружок. 1-й год >> Задачник первого года >> Задачи с целыми числами | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок. Задачник первого года. Задачи с целыми числами |
|
|
Если каждый мальчик купит пирожок, а каждая девочка – булочку, то они потратят вместе на одну копейку меньше, чем если бы каждый мальчик купил булочку, а каждая девочка – пирожок. Известно, что мальчиков больше, чем девочек. На сколько?
Задача 65:
175 Шалтаев стоят дороже, чем 125, но дешевле, чем 126 Болтаев. Докажите, что на трех Шалтаев и одного Болтая рубля не хватит.
Задача 66:
В классе каждый мальчик дружит с тремя девочками, а каждая девочка – с двумя мальчиками. При этом в классе всего 19 парт и 31 пионер. Сколько в классе учеников?
Задача 67:
Две команды разыграли первенство школы в десяти видах, причем за победу команда получала 4 очка, за ничью – 2 и за проигрыш – 1 очко. Вместе обе команды набрали 46 очков. Сколько было ничьих?
Задача 68:
Четверо товарищей купили вместе лодку. Первый внес половину суммы, внесенной остальными; второй – треть суммы, внесенной остальными; третий – четверть суммы, внесенной остальными, а четвертый внес 130 рублей. Сколько стоит лодка и сколько внес каждый?
Задача 69:
На дороге, соединяющей два аула, нет горизонтальных участков. Автобус идет в гору всегда со скоростью 15 км/ч, а под гору – 30 км/ч. Найдите расстояние между аулами, если известно, что путь туда и обратно автобус проезжает за 4 часа.
Задача 70:Существуют ли такие натуральные a и b, что ab(a – b) = 45045?
Задача 71:
Обозначим сумму трех последовательных натуральных чисел через a, а сумму трех следующих за ними натуральных чисел – через b. Может ли произведение ab равняться 111111111?
Задача 72:
Докажите, что последняя ненулевая цифра числа 1985! четна.
Задача 73:
Натуральные числа x и y таковы, что 34x = 43y. Докажите, что число x + y – составное.
Задача 74:
Существуют ли такие целые числа a и b, отличные от нуля, что одно из них делится на их сумму, а другое – на их разность?
Задача 75:
Простые числа p и q и натуральное число n удовлетворяют соотношению

Задача 76:
Докажите, что натуральное число, десятичная запись которого состоит из одной единицы, двух двоек, трех троек, …, девяти девяток, не может быть точным квадратом.
Задача 77:
Каждое из натуральных чисел a, b, c и d делится на ab – cd. Докажите, что ab – cd равно 1 или – 1.
Задача 78:
В стране Анчурии в обращении имеются купюры четырех достоинств: 1 доллар, 10 долларов, 100 долларов, 1000 долларов. Можно ли отсчитать миллион долларов так, чтобы получилось ровно полмиллиона купюр?
Задача 79:
На доске написано число 1. Каждую секунду к числу на доске прибавляют сумму его цифр. Может ли через некоторое время на доске появиться число 123456?
Задача 80:
Докажите, что число 3999991 не является простым.
Задача 81:
а) Найдите семизначное число, все цифры которого различны и которое делится на все эти цифры.
б) Существует ли такое восьмизначное число?
Задача 82:
У числа 19¹ºº вычисляют сумму цифр, после этого у полученного числа подсчитывают сумму цифр и так далее, до тех пор, пока не получится однозначное число. Какое оно?
Задача 83:
Докажите, что остаток от деления простого числа на 30 – простое число или единица.
Задача 84:
Существует ли натуральное число, произведение цифр которого равно 1980?
Задача 85:
Некоторое число оканчивается на 2. Если эту цифру перенести в начало числа, то число удвоится. Найдите наименьшее такое число.
Задача 86:
Дано шестизначное число 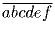 , причем
, причем
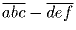 делится
на 7. Докажите, что и само число делится на 7.
делится
на 7. Докажите, что и само число делится на 7.
Задача 87:
Найдите минимальное натуральное число, которое в 4 раза меньше числа, записанного теми же цифрами, но в обратном порядке.
Задача 88:
Дано трехзначное число, у которого первая и последняя цифры разнятся не менее, чем на 2. Составляется разность этого числа и числа ему обращенного (т.е. числа, записанного теми же цифрами, но в обратном порядке). К результату прибавляется число ему обращенное. Докажите, что полученная сумма равна 1089.
Задача 89:
Что больше: 2³ºº или 3²ºº?
Задача 90:
Что больше: 31¹¹ или 1714?
Задача 91:
Что больше: 5099 или 99! ?
Задача 92:
Что больше: 888 … 88 × 333 … 33 или 444 … 44 × 666 … 67 (каждое из чисел записано 1989 цифрами)?
Задача 93:
Каких 6-значных чисел больше: тех, которые представляются в виде произведения двух трехзначных чисел, или остальных?
Задача 94:Дано несколько одинаковых картонных треугольников. В вершинах каждого из них написаны числа 1, 2 и 3. Треугольники сложены в ровную стопку. Может ли оказаться так, что суммы чисел вдоль каждого вертикального ребра стопки равны 55?
Задача 95:
Можно ли расположить по окружности 15 целых чисел так, чтобы сумма любых четырех чисел подряд равнялась 1 или 3?
Задача 96:
Найдите тысячу натуральных чисел таких, что их сумма равна их произведению.
Задача 97:
Подряд выписаны числа 21989 и 51989. Сколько всего выписано цифр?
Задача 98:
Автобусный билет называется счастливым, если сумма первых его трех цифр равна сумме трех последних. Докажите, что счастливых билетов столько же, сколько билетов с суммой всех шести цифр, равной 27.
| Задачная база >> Разное >> Математический кружок. 1-й год >> Задачник первого года >> Задачи с целыми числами | Убрать решения |