 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Делимость-2 >> Десятичная запись и признаки делимости | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Делимость-2. Десятичная запись и признаки делимости |
|
|
Докажите, что любое натуральное число сравнимо со своей последней цифрой по модулю а) 10; б) 2; в) 5.
Решение:
Вычтем из числа его последнюю цифру и получим число, оканчивающееся нулем, т.е. делящееся на 10 (а значит, и на 5, и на 2).
Задача 25:
Докажите, что 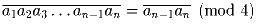 .
.
Решение:
Указание: все степени десяти, начиная со 100, делятся на 4.
Задача 26:Сформулируйте и докажите признаки делимости на 2n и 5n.
Решение:
Число делится на 2n (на 5n) тогда и только тогда, когда число, образованное его последними n цифрами, делится на 2n (на 5n).
Задача 27:Последняя цифра квадрата натурального числа равна 6. Докажите, что его предпоследняя цифра нечетна.
Решение:
Так как последняя цифра 6, то возводимое в квадрат число четно. Раз оно является квадратом, то оно делится и на 4. Следовательно, число, составленное из двух его последних цифр, должно делиться на 4. Все требуемые двузначные числа легко выписать: 16, 36, 56, 76, 96.
Задача 28:
Предпоследняя цифра квадрата натурального числа – нечетная. Докажите, что его последняя цифра 6.
Решение:
Две последние цифры квадрата числа n зависят только от
двух последних цифр числа n. Пусть 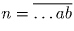 . Тогда
. Тогда
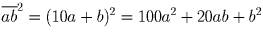 . Ясно, что цифра десятков
числа b² должна быть нечетной. Прямой перебор показывает, что
цифра единиц должна тогда быть равной 6.
. Ясно, что цифра десятков
числа b² должна быть нечетной. Прямой перебор показывает, что
цифра единиц должна тогда быть равной 6.
Докажите, что степень двойки не может оканчиваться четырьмя одинаковыми цифрами.
Решение:
Рассмотрите остатки по модулю 16.
Задача 30:
Найдите 100-значное число без нулевых цифр, которое делится на сумму своих цифр.
Решение:
Подберем число так, чтобы сумма его цифр равнялась 125. Делимость числа на 125 определяется тремя его последними цифрами. Следовательно, годится число 111 … 11599125 (в начале записи единица написана 94 раза).
Задача 31:Докажите, что любое натуральное число сравнимо с суммой своих цифр по модулю а) 3; б) 9.
Решение:
Рассмотрим число
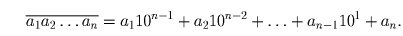
Можно ли записать точный квадрат, использовав по 10 раз цифры а) 2, 3, 6; б) 1, 2, 3 ?
Решение:
а) нет; б) нет. Рассмотрите остатки по модулю 9.
Задача 33:У числа 2¹ºº нашли сумму цифр, у результата снова нашли сумму цифр и т.д. В конце концов получилось однозначное число. Найдите его.
Решение:
7.
Задача 34:Докажите, что если записать в обратном порядке цифры любого натурального числа, то разность исходного и нового числа будет делиться на 9.
Решение:
Эти числа имеют одинаковые суммы цифр и, значит, одинаковые остатки по модулю 9.
Задача 35:К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.
Решение:
Это можно сделать шестью способами: 1155, 4155, 7155, 3150, 6150, 9150.
Задача 36:
Сколько имеется четырехзначных чисел, которые делятся на 45, а две средние цифры у них – 97?
Решение:
Два числа: 6975, 2970.
Задача 37:
Найдите наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.
Решение:
Это число 1023457896.
Задача 38:Докажите, что произведение последней цифры числа 2n и суммы всех цифр этого числа, кроме последней, делится на 3.
Решение:
Разберите два случая: последняя цифра равна или не равна 6.
Задача 39:
Может ли сумма цифр точного квадрата равняться 1970?
Решение:
Нет. Рассмотрите остатки по модулю 3.
Задача 40:Из трехзначного числа вычли сумму его цифр. С полученным числом проделали то же самое и так далее, 100 раз. Докажите, что в результате получится нуль.
Решение:
7.
Задача 41:Пусть A – сумма цифр числа 44444444, а B – сумма цифр числа A. Найдите сумму цифр числа B.
Решение:
7.
Задача 42:
Докажите, что
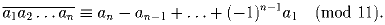
Решение:
Указание: 10 ≡ – 1 (mod 11).
Задача 43:
Докажите, что число 111 … 11 (2n единиц) – составное.
Решение:
Это число делится на 11.
Задача 44:Докажите, что число 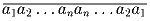 – составное.
– составное.
Решение:
Это число делится на 11.
Задача 45:Пусть a, b, c, d – различные цифры. Докажите, что
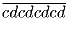 не делится на
не делится на 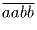 .
.
Решение:
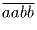 делится на 11, а
делится на 11, а 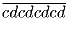 – нет.
– нет.
A – шестизначное число, в записи которого по одному разу встречаются цифры 1, 2, 3, 4, 5, 6. Докажите, что A не делится на 11.
Решение:
Цифры 1, 2, 3, 4, 5, 6 нельзя разбить на две тройки, разность сумм в которых делится на 11.
Задача 47:Докажите, что разность числа, имеющего нечетное количество цифр, и числа, записанного теми же цифрами, но в обратном порядке, делится на 99.
Решение:
Эти два числа имеют одинаковые остатки как при делении на 9, так и при делении на 11.
Задача 48:
Можно ли составить из цифр 2, 3, 4, 9 (каждую цифру можно использовать сколько угодно раз) два числа, одно из которых в 19 раз больше другого?
Решение:
Нельзя. Проследите за последней цифрой.
Задача 49:
Сумма двух цифр a и b делится на 7. Докажите, что
число 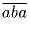 также делится на 7.
также делится на 7.
Решение:
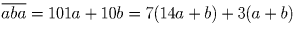 .
.
Сумма цифр трехзначного числа равна 7. Докажите, что это число делится на 7 тогда и только тогда, когда две его последние цифры равны.
Решение:
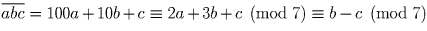 , так
как 2(a + b + c) ≡ 0 (mod 7). Значит,
, так
как 2(a + b + c) ≡ 0 (mod 7). Значит, 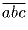 делится на 7
тогда и только тогда, когда b – c делится на 7. Но так как b,
c < 7, то это условие равносильно тому, что b = c.
делится на 7
тогда и только тогда, когда b – c делится на 7. Но так как b,
c < 7, то это условие равносильно тому, что b = c.
а) Дано шестизначное число 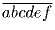 , причем
, причем
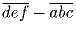 делится на 7. Докажите, что и само число делится на 7.
делится на 7. Докажите, что и само число делится на 7.
б) Сформулируйте и докажите признак делимости на 7.
в) Сформулируйте и докажите признак делимости на 13.
Решение:
а) 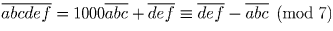 , так как 1001 делится на 7.
, так как 1001 делится на 7.
б), в) Число делится на 7 (13) тогда и только тогда, когда на 7 (13) делится знакопеременная сумма чисел, образованных последовательными тройками цифр данного числа. Пример: 10345678. Образуем знакопеременную сумму: 678 – 345 + 10 = 343 – делится на 7. Значит, и исходное число делится на 7. И в самом деле, оно равно 7 • 1477954.
Задача 52:а) Дано шестизначное число 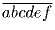 , причем
, причем
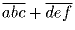 делится на 37. Докажите, что и само число
делится на 37.
делится на 37. Докажите, что и само число
делится на 37.
б) Сформулируйте и докажите признак делимости на 37.
Решение:
Число делится на 37 тогда и только тогда, когда сумма чисел, образованных тройками последовательных цифр данного числа, должна делиться на 37.
Задача 53:Существует ли такое трехзначное число 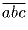 , что
, что
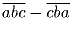 является квадратом натурального числа?
является квадратом натурального числа?
Решение:
Нет, не существует. 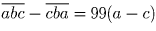 , где a
и c – разные цифры.
, где a
и c – разные цифры.
Найдите наименьшее число, записываемое одними единицами, делящееся на 333 … 33 (в записи 100 троек).
Решение:
Запись этого числа состоит из 300 единиц.
Задача 55:Может ли сумма нескольких первых натуральных чисел оканчиваться на 1989?
Решение:
Нет. Рассмотрите остатки по модулю 5.
Задача 56:Найдите все натуральные числа, которые увеличиваются в 9 раз, если между цифрой единиц и цифрой десятков вставить ноль.
Решение:
Запишем наше число в виде 10a + b, где b – цифра единиц. Получим уравнение 100a + b = 9(10a + b). Отсюда 10a = 8b, т.е. 5a = 4b. Таким образом, b делится на 5. Рассмотрев два случая b = 0, b = 5, получаем единственный ответ: 45.
Задача 57:Между цифрами двузначного числа, кратного трем, вставили нуль, и к полученному трехзначному числу прибавили удвоенную цифру его сотен. Получилось число, в 9 раз большее первоначального. Найдите исходное число.
Решение:
69.
Задача 58:Найдите четырехзначное число, являющееся точным квадратом, первые две цифры которого равны между собой и последние две цифры которого также равны между собой.
Решение:
7744 = 88².
Задача 59:Найдите все трехзначные числа, каждая натуральная степень которых оканчивается на три цифры, составляющие первоначальное число.
Решение:
625 и 376.
Задача 60:К числу справа приписывают тройки. Докажите, что когда-нибудь получится составное число.
Решение:
Рассмотрите остатки по модулю 7.
Задача 61:
Докажите, что все числа ряда 10001,100010001,1000100010001, … являются составными.
Решение:
Домножьте число на 1111 и докажите, что результат делится на число вида 1000 …001.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Делимость-2 >> Десятичная запись и признаки делимости | Убрать решения |