 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Геометрия >> Два неравенства | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Геометрия. Два неравенства |
|
|
Докажите, что при b + c > a, a + c > b, a + b > c, где a, b и c – положительные числа, существует треугольник со сторонами a, b и c.
Решение:
Указание: выясните, какой может быть длина третьей стороны в треугольнике, две стороны которого имеют длины a и b.
Задача 2:Докажите, что медиана AM в треугольнике ABC по длине больше, чем (AB + AC – BC)/2.
Решение:
Указание: докажите неравенства AM > AB – BC/2 и AM > AC – BC/2.
Задача 3:Докажите, что из отрезков длины a, b и c можно составить треугольник тогда и только тогда, когда есть такие положительные x, y, z, что a = x + y, b = y + z, c = x + z.
Решение:
Указание: рассмотрите окружность, вписанную в треугольник, и длины отрезков, на которые точки касания делят стороны.
Задача 4:Докажите, что если AB = AC, то углы ABC и ACB равны.
Решение:
Указание: проведите доказательство от противного.
Задача 5:
В треугольнике ABC длина медианы AM больше половины длины BC. Докажите, что угол BAC – острый.
Решение:
Указание: используйте неравенства ∠ BAM > ∠ ABM и ∠ CAM > ∠ ACM.
Задача 6:Докажите, что если из отрезков длины a, b и c можно
составить треугольник,то его можно составить и из отрезков длины
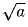 ,
, 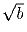 ,
, 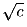 .
.
Решение:
Это простое упражнение на применение неравенства треугольника.
Задача 7:
ABCD – выпуклый 4-угольник, причем AB + BD < AC + CD. Докажите, что AB < AC.
Решение:
Так как AB + CD < AC + BD (кстати, почему?), то, складывая это неравенство с данным в условии, получаем требуемое.
Задача 8:Центры трех непересекающихся кругов расположены на одной прямой. Докажите, что если окружность касается всех кругов, то ее радиус больше радиуса одного из них.
Решение:
1. Можно считать, что все касания внешние иначе утверждение задачи очевидно. Тогда, если мы обозначим радиусы окружностей с центрами A, B, C и D соответственно через r1, r2, r3 и R, то по неравенству треугольника AD + DC > AC, то есть R + r1 + R + r3 > AC > r1 + r3 + 2r2 и значит, R > r2, ч.т.д.
2. Один из углов DBA и DBC – неострый и значит, наибольший в соответствующем треугольнике. Пусть это угол DBA. Тогда по неравенству 2 DA > AB, т.е. R + r1 > AB > r1 + r2 и значит, R > r2, ч.т.д.
Задача 9:Пусть ABCD и A1B1C1D1 – два выпуклых 4-угольника с соответственно равными сторонами. Докажите, что если ∠ A > ∠ A1, то ∠ B < ∠ B1, ∠ C > ∠ C1, ∠ D < ∠ D1.
Решение:
Раз ∠ A > ∠ A1, то BD > B1D1, и значит ∠ C > ∠ C1. Если же ∠ B > ∠ B1, то аналогично ∠ D > ∠ D1, чего быть не может, так как сумма углов в четырехугольниках одна и та же.
Задача 10:Докажите, что медиана треугольника, заключенная между двумя его неравными сторонами, образует больший угол с меньшей из двух этих сторон.
Решение:
Надо достроить треугольник ABC до параллелограмма ABDC и применить неравенство о большей стороне и большем угле.
Задача 11:Могут ли в прямолинейной пятиконечной звезде ABCDEFGHIK выполняться неравенства: AB > BC, CD > DE, EF > FG, GH > HI, IK > KA?
Решение:Из неравенства о большей стороне и большем угле следует, что ∠ BAC > ∠ BCA = ∠ DCE > ∠ DEC = … > ∠ KAI = ∠ BAC – противоречие!
Задача 12:Дан равнобедренный треугольник ABC с углом при вершине B, равным 20 градусов. Докажите, что а) AB < 3AC; б) AB > 2AC.
Решение:
а) Приложите друг к другу боковыми сторонами три копии данного треугольника. б) Отложите на стороне AB отрезок AE, равный основанию AC, и докажите, что EB > CE > AC.
Задача 13:Периметр пятиконечной звезды с вершинами в вершинах выпуклого пятиугольника Ф, периметр самого Ф, и периметр внутреннего пятиугольника звезды – простые числа. Докажите, что их сумма не меньше 20.
Решение:
Если обозначить три указанных периметра через a, b, c, то a > c, a + c < b, 2a > b. Дальше действуйте перебором.
Задача 14:
На каждой стороне квадрата отмечено по точке. Докажите, что периметр образованного ими четырехугольника не меньше удвоенной длины диагонали квадрата.
Решение:
«Разверните» периметр четырехугольника, как это показано
| Задачная база >> Разное >> Математический кружок. 2-й год >> Геометрия >> Два неравенства | Убрать решения |