 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Графы-2 >> Теорема Эйлера | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Графы-2. Теорема Эйлера |
|
|
В стране Озерная 7 озер, соединенных между собой 10 каналами, причем от любого озера можно доплыть до любого другого. Сколько в этой стране островов?
Решение:
4.
Задача 18:
В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?
Решение:
Будем считать отмеченные точки и вершины квадрата вершинами, а соединяющие их отрезки и стороны квадрата – ребрами плоского графа. Для каждого куска, на которые этот граф разбивает плоскость, подсчитаем число ограничивающих его ребер, и все полученные числа сложим. Поскольку каждое ребро разделяет два куска, то в итоге получим удвоенное число ребер. Так как все куски, кроме внешнего – треугольники, а внешний кусок ограничен 4 ребрами, то получаем 3(F – 1) + 4 = 2E, т.е. E = 3(F – 1)/2 + 2. Заметим, что число вершин нашего графа равно 24 и подставим количества вершин и ребер в формулу Эйлера:
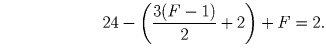
Задача 19:
Докажите, что для плоского графа справедливо неравенство 2E ≥ 3F.
Решение:
Указание: каждый кусок ограничивается не менее, чем тремя ребрами.
Задача 20:Для плоского связного графа справедливо неравенство E ≤ 3V – 6.
Решение:
Из предыдущей задачи известно, что 2E ≥ 3F. Подставим это в формулу Эйлера. Получим V – E + 2E/3 ≥ 2. Отсюда E ≤ 3V – 6, что и требовалось.
Задача 21:
Докажите, что для любого плоского графа (в том числе и несвязного) справедливо неравенство E ≤ 3V – 6.
Решение:
Указание: Требуемое утверждение получается сложением неравенств для компонент связности.
Задача 22:
Граф, имеющий 5 вершин, каждая из которых соединена ребром с любой другой, не является плоским.
Решение:Указание: Для этого графа не выполнено неравенство E ≤ 3V – 6.
Задача 23:Можно ли построить три дома, вырыть три колодца и соединить тропинками каждый дом с каждым колодцем так, чтобы тропинки не пересекались?
Решение:Указание: Для графа из этой задачи неравенство 2E ≥ 3F можно усилить. Поскольку в этом графе каждый кусок должен быть ограничен по меньшей мере 4 ребрами, то рассуждения, аналогичные решению задачи 19, приводят к неравенству E ≥ 2F.
Задача 24:
Докажите, что граф, имеющий 10 вершин, степень каждой из которых равна 5, – не плоский.
Решение:
Не выполняется неравенство 3V – 6 ≥ E.
Задача 25:
Докажите, что в плоском графе есть вершина, степень которой не превосходит 5.
Решение:
Предположим противное. Тогда 2E ≥ 6V, т.е. E ≥ 3V, что противоречит неравенству.
Задача 26:Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо «красный», либо «синий» граф не является плоским.
Решение:
Пусть оба эти графа – плоские. Тогда у них вместе не более, чем (3 • 11 – 6) + (3 • 11 – 6) = 54 ребра. Однако в полном графе с 11 вершинами 55 ребер. Противоречие.
Задача 27:Семиугольник разбит на выпуклые пяти- и шестиугольники, причем так, что каждая его вершина является вершиной по крайней мере двух многоугольников разбиения. Докажите, что число пятиугольников разбиения не меньше 13.
Решение:
Докажите сначала неравенство E ≤ 3V – 6, используя то, что из каждой вершины выходит по крайней мере 3 ребра. Обозначим количество пятиугольников через a, количество шестиугольников через b. Заметим, что 5a + 6b + 7 = 2E ≤ 6F – 12 = 6(a + b + 1) – 12. Отсюда a ≥ 13.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Графы-2 >> Теорема Эйлера | Убрать решения |