 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Графы-2 >> Разные задачи | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Графы-2. Разные задачи |
|
|
Докажите, что связный граф, имеющий не более двух нечетных вершин, можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро ровно один раз.
Решение:План решения: Разберем случай, когда граф не имеет нечетных вершин. Проведем доказательство с помощью индукции по числу ребер графа. База (граф без ребер) очевидна. Для доказательства индукционного перехода рассмотрим произвольный связный граф, степени всех вершин которого четны. Поскольку в этом графе нет висячих вершин, то он не является деревом, и следовательно, в нем есть цикл. Временно удалим из графа ребра этого цикла. Ясно, что граф распадется на несколько компонент связности, имеющих общие вершины с выкинутым циклом и удовлетворяющих условиям теоремы. В силу индукционного предположения каждую из этих компонент связности можно нарисовать требуемым образом. Теперь ясно как нарисовать требуемым образом исходный граф: обходим цикл и попадая в вершину, относящуюся к какой-то компоненте, переходим в нее и рисуем ее, в конце возвращаясь в ту же вершину, после чего продолжаем движение по циклу.
Доказательство для случая графа с двумя нечетными вершинами аналогично (нужно временно удалить путь, соединяющий две нечетные вершины).
Задача 29:
Можно ли составить решетку, изображенную на рисунке.
а) из 5 ломаных длины 8?
б) из 8 ломаных длины 5? (длина стороны клетки равна 1).
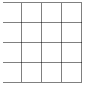
а) Нельзя – 12 нечетных вершин. б) Можно.
Задача 30:На плоскости дано 100 окружностей, составляющих связную (т.е. не распадающуюся на части) фигуру. Докажите, что эту фигуру можно нарисовать, не отрывая карандаша от бумаги и не проводя дважды одну и ту же линию.
Решение:
Граф связен, степени всех его вершин четны.
Задача 31:Докажите, что связный граф с 2n нечетными вершинами можно нарисовать, оторвав карандаш от бумаги ровно n – 1 раз и не проводя никакое ребро дважды.
Решение:
Доказательство можно провести индукцией по n. Для доказательства индукционного перехода выберем две нечетные вершины, соединим их путем и временно удалим все его ребра. Граф распадется на компоненты связности. Присоединим теперь к удаленному пути компоненты связности, которые, очевидно, не содержат нечетных вершин.
Задача 32:На конференции присутствуют 50 ученых, каждый из которых знаком по крайней мере с 25 участниками конференции. Докажите, что найдутся четверо из них, которых можно усадить за круглый стол так, чтобы каждый сидел рядом со знакомыми ему людьми.
Решение:
Рассмотрите двух незнакомых ученых и их знакомых.
Задача 33:Каждый из 102 учеников одной школы знаком не менее, чем с 68 другими. Докажите, что среди них найдутся четверо, имеющие одинаковое число знакомых.
Решение:
Предположим противное. Тогда для каждого числа от 68 до 101 есть ровно три человека, имеющие такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.
Задача 34:Расстоянием между двумя произвольными вершинами дерева будем называть длину простого пути, соединяющего их. Удаленностью вершины дерева назовем сумму расстояний от нее до всех остальных вершин. Докажите, что в дереве, у которого есть две вершины с удаленностями, отличающимися на 1, – нечетное число вершин.
Решение:
Соединим эти две вершины путем. Пусть a – его длина. Расстояние от любой вершины до двух данных отличаются на величину, имеющую ту же четность, что и a.
Задача 35:Дима нарисовал на доске 7 графов, каждый из которых является деревом с 6 вершинами. Докажите, что среди них есть два изоморфных.
Решение:
Найдите такую шестёрку графов, что любое дерево с 6 вершинами изоморфно одному из них.
Задача 36:В некоторой стране любые два города соединены либо авиалинией, либо железной дорогой. Докажите, что
а) можно выбрать вид транспорта так, чтобы от любого города можно было добраться до любого другого, пользуясь только этим видом транспорта;
б) из некоторого города, выбрав один из видов транспорта, можно добраться до любого другого города не более, чем с одной пересадкой (пользоваться можно только выбранным видом транспорта);
в) каждый город обладает свойством из пункта б);
г) можно выбрать вид транспорта так, чтобы пользуясь только им, можно было добраться из любого города до любого другого не более, чем с двумя пересадками.
Решение:
в) Рассмотрите произвольный город X, город A, в который из X нельзя долететь не более, чем с одной пересадкой, и город B, в который из X нельзя доехать на поезде не более, чем с одной пересадкой. Заметьте, что эти города соединены каким-то видом транспорта. г) Пусть из A в B нельзя долететь не более, чем с двумя пересадками; из C в D нельзя доехать на поезде не более, чем с двумя пересадками. Рассмотрите граф сообщений четырех упомянутых городов.
Задача 37:Каждое из ребер полного графа с 6 вершинами покрашено в один из двух цветов. Докажите, что есть три вершины, все ребра между которыми – одного цвета.
Решение:
Среди рёбер, выходящих из данной вершины, можно найти три ребра одного цвета. Среди трех вершин, в которые ведут эти рёбра, или какие-то две соединены ребром того же цвета, тогда они вместе с выбранной нами исходно образуют нужную тройку, либо они все рёбра между ними одноцветны.
Задача 38:
Каждое из ребер полного графа с 17 вершинами покрашено в один из трех цветов. Докажите, что есть три вершины, все ребра между которыми – одного цвета.
Решение:
Из произвольной вершины выходит по крайней мере 6 ребер одного цвета. К вершинам, в которые ведут эти рёбра, можно применить предыдущую задачу.
Задача 39:Каждое из ребер полного графа с 9 вершинами покрашено в синий или красный цвет. Докажите, что либо есть четыре вершины, все ребра между которыми – синие, либо есть три вершины, все ребра между которыми – красные.
Решение:
Пусть есть вершина, из которой выходит 6 синих ребер. Тогда воспользуемся результатом задачи 37. Пусть есть вершина, из которой выходит не более 4 синих ребер (из всех 9-ти вершин не может выходить по 5 синих ребер). Тогда из нее выходит по крайней мере 4 красных ребра.
Задача 40:Каждое из ребер полного графа с 18 вершинами покрашено в один из двух цветов. Докажите, что есть четыре вершины, все ребра между которыми – одного цвета.
Решение:Из произвольной вершины выходит по крайней мере 9 ребер одного цвета.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Графы-2 >> Разные задачи | Убрать решения |