 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Инвариант >> Инвариант -- остаток | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Инвариант. Инвариант -- остаток |
|
|
Иван-царевич имеет два волшебных меча, один из которых может отрубить Змею Горынычу 21 голову, а второй – 4 головы, но тогда у Змея Горыныча отрастает 1985 голов. Может ли Иван отрубить Змею Горынычу все головы, если в самом начале у него было 100 голов? (Примечание: если, например, у Змея Горыныча осталось лишь три головы, то рубить их ни тем, ни другим мечом нельзя).
Решение:
Инвариант – остаток числа голов Змея Горыныча по модулю 7.
Задача 17:В странах Диллии и Даллии денежными единицами являются диллеры и даллеры соответственно, причем в Диллии диллер меняется на 10 даллеров, а в Даллии даллер меняется на 10 диллеров. Начинающий финансист имеет 1 диллер и может свободно перезжать из одной страны в другую и менять свои деньги в обеих странах. Докажите, что количество даллеров у него никогда не сравняется с количеством диллеров.
Решение:
Инвариант – остаток по модулю 11 разности между числом диллеров и число даллеров у финансиста.
Задача 18:Разменный автомат меняет одну монету на пять других. Можно ли с его помощью разменять металлический рубль на 26 монет?
Решение:
Нельзя. Проследите за остатками по модулю 4.
Задача 19:Есть три печатающих автомата. Первый по карточке с числами a и b выдает карточку с числами a + 1 и b + 1; второй по карточке с четными числами a и b выдает карточку с числами a/2 и b/2; третий автомат по паре карточек с числами a,b и b,c выдает карточку с числами a,c. Все автоматы возвращают заложенные в них карточки. Можно ли с помощью этих автоматов из карточки (5, 19) получить карточку (1, 1988)?
Решение:
Попробуем промоделировать сам процесс решения задачи.
Итак, внешний вид задачи: дан набор разрешенных операций и нас просят выяснить, можно ли из одной карточки получить другую – наталкивает нас на то, что нужно искать инвариант. Начнем поиск.
1-я операция: (a,b) → (a + 1,b + 1). Что же не меняется при этой операции? Ну, конечно же, разность чисел на карточке: (a + 1) – (b + 1) = a – b. Но вот уже 2-я операция меняет разность: a/2 – b/2 = (a – b)/2 – она делит ее пополам. 3-я операция складывает эти разности: a – c = (a – b) + (b – c).
Все это приводит нас к мысли, что, видимо, инвариантом является не сама разность, а… что же? Что можно сделать с этим числом? Вполне возможно, что ответ на этот вопрос не сразу придет вам на ум. Ну что же, займемся небольшим исследованием. Наудачу попробуем получить какие-то карточки из данной:
Пока хватит. Теперь уже можно посмотреть на плоды наших трудов. Мы имеем набор карточек: (5, 19), (6, 20), (3, 10), (20, 27), (6, 27). Вычислим для них разность чисел на карточке и получим набор чисел: 14, 14, 7, 7, 21. Тут, конечно, мы сразу догадались, что нужно доказывать! Конечно же то, что наша разность a – b всегда будет делиться на 7. Доказывается это очень просто, стоит только еще раз посмотреть, что происходит с разностью при разрешенных операциях (см. выше). Но у той карточки, которую нам хочется получить – (1, 1988) – разность чисел равна 1 – 1988 = – 1987 и на 7 не делится. Задача решена.
Задача 20:
На доске написано число 8n. У него вычисляется сумма цифр, у полученного числа вновь вычисляется сумма цифр, и так далее, до тех пор, пока не получится однозначное число. Что это за число, если n = 1989?
Решение:
Используйте то, что у суммы цифр тот же остаток при делении на 9, что и у самого числа.
Задача 21:В пробирке находятся марсианские амебы трех типов: A, B и C. Две амебы любых двух разных типов могут слиться в одну амебу третьего типа. После нескольких таких слияний в пробирке оказалась одна амеба. Каков ее тип, если исходно амеб типа A было 20 штук, типа B – 21 штука и типа C – 22 штуки?
Решение:
Ее тип – B. Проследите за четностью разностей N(A) – N(B), N(B) – N(C), N(C) – N(A), где N(X) – число амеб типа X.
Задача 22:
Фишка ходит по квадратной доске, каждым своим ходом сдвигаясь либо на клетку вверх, либо на клетку вправо, либо по диагонали вниз-влево. Может ли она обойти всю доску, побывав на всех полях ровно по одному разу, и закончить на поле, соседнем справа от исходного?
Решение:
Сумма номеров строки и столбца при каждом ходе либо уменьшается на 2, либо увеличивается на 1. Значит, ее остаток по модулю 3 каждый раз увеличивается на 1. Так как всего ходов n² – 1, а в конце сумма должна быть на 1 больше исходной, то мы получаем, что n² – 2 должно делиться на 3, что невозможно. Следовательно, такого обхода нет.
Задача 23:В таблице m × n расставлены числа так, что сумма чисел в любой строке или столбце равна 1. Докажите, что m = n. Примечание. Как ни странно, но в некотором смысле это тоже задача на инвариант.
Решение:
Сумма чисел в таблице не зависит от способа ее подсчета. Именно в этом смысле это – задача на инвариант.
Задача 24:На столе стоят 7 стаканов – все вверх дном. Разрешается за один ход перевернуть любые 4 стакана. Можно ли за несколько ходов добиться того, чтобы все стаканы стояли правильно?
Решение:
Нельзя. Инвариантом служит четность числа неправильно стоящих стаканов;
Задача 25:
В вершинах куба расставлены числа: 7 нулей и одна единица. За один ход разрешается прибавить по единице к числам в концах любого ребра куба. Можно ли добиться того, чтобы все числа стали равными? А можно ли добиться того, чтобы все числа делились на 3?
Решение:
Нельзя. Нужно пометить четыре вершины куба такие, что никакие две из них не соединены ребром, после чего рассмотреть разность между суммой чисел в помеченных вершинах и суммой чисел в непомеченных вершинах;
Задача 26:
Круг разделен на 6 секторов, как в задаче 3, и в них по часовой стрелке расставлены числа: 1, 0, 1, 0, 0, 0. Разрешается прибавить по единице к числам в любых двух соседних секторах. Можно ли такими операциями добиться того, чтобы все числа в секторах были одинаковыми?
Решение:
Нельзя. Нужно занумеровать сектора числами от 1 до 6 по порядку, после чего рассмотреть разность между суммой чисел в «четных» секторах и суммой чисел в «нечетных» секторах.
Задача 27:В задаче 20 выясните, какие карточки можно получить из карточки (5, 19), а какие нельзя.
Решение:
В точности те (a,b), для которых a < b и b – a делится на 7.
Задача 28:На столе лежит куча из 1001 камня. Ход состоит в том, что из какой-либо кучи, содержащей более одного камня, выкидывают камень, а затем одну из куч делят на две. Можно ли через несколько ходов оставить на столе только кучки, состоящие из трех камней?
Решение:
Нельзя. Рассмотрите величину s, равную сумме числа камней и числа куч.
Задача 29:В ряд выписаны числа 1, 2, 3, …, n. За один ход разрешается поменять местами любые два числа. Может ли после 1989 таких операций порядок чисел оказаться исходным?
Решение:
Нет, не может. В качестве инварианта рассмотрите четность величины p, равной числу пар (a,b), в которых число a стоит правее числа b и при этом a > b.
Задача 30:Дана некоторая тройка чисел. С любыми двумя из них
разрешается проделывать следующее: если эти числа равны a и
b, то их можно заменить на 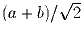 и
и 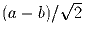 . Можно
ли с помощью таких операций получить тройку
. Можно
ли с помощью таких операций получить тройку  из тройки
из тройки 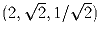 ?
?
Решение:
Нельзя. Рассмотрите сумму квадратов чисел тройки.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Инвариант >> Инвариант -- остаток | Убрать решения |