 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Комбинаторика-2 >> Шары и перегородки | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Комбинаторика-2. Шары и перегородки |
|
|
6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?
Решение:
Выложим шары в ряд. Для определения расклада наших
шаров по шести ящикам разделим ряд пятью перегородками на шесть
групп: первая группа для первого ящика, вторая – для второго и
так далее. Таким образом, число вариантов раскладки шаров по
ящикам равно числу способов расположения пяти перегородок.
Перегородки могут стоять на любом из 19 мест (между 20 шарами –
19 промежутков). Поэтому число их возможных расположений
равно 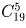 .
.
Задача 32:
6 ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?
Решение:
Рассмотрим ряд из 25 предметов: 20 одинаковых шаров и 5
одинаковых перегородок, расположенных в произвольном порядке.
Каждый такой ряд однозначно соответствует некоторому способу
раскладки шаров по ящикам: в первый ящик попадают шары,
расположенные левее первой перегородки, во второй – расположенные
между первой и второй перегородками и т.д. (между какими-то
перегородками шаров может и не быть). Поэтому число способов
раскладки шаров по ящикам равно числу различных рядов из 20 шаров
и 5 перегородок, т.е. равно 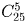 (ряд определяется теми пятью
местами из 25, на которых стоят перегородки).
(ряд определяется теми пятью
местами из 25, на которых стоят перегородки).
Сколькими способами натуральное число n можно представить в виде суммы
а) k натуральных слагаемых;
б) k неотрицательных целых слагаемых (представления, отличающиеся порядком слагаемых, считаются различными)?
Решение:
Указание. Представим n в виде суммы n единиц:
n = 1 + 1 + … + 1. Назовем теперь эти n единиц «шарами», а k
слагаемых из условия задачи – «ящиками». Ответ: а) 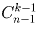 ; б)
; б) 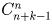 .
.
Задача 34:
Сколькими способами 12 пятаков можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не оказался пустым?
Решение:
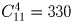 .
.
Переплетчик должен переплести 12 одинаковых книг в красный, зеленый или синий переплеты. Сколькими способами он может это сделать?
Решение:
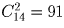 .
.
Сколькими способами можно разрезать ожерелье, состоящее из 30 различных бусин на 8 частей (резать можно только между бусинами)?
Решение:Нужно указать 8 мест из 30, в которых будут произведены
разрезы. Ответ: 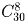 .
.
Задача 37:
30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует только за одно предложение и учитывается лишь количество голосов, поданных за каждое предложение?
Решение:
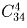 .
.
В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить в нем
а) 12 открыток;
б) 8 открыток;
в) 8 различных открыток?
Решение:
а) 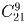 ; б)
; б) 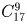 ; в) 10!/2! = 1814400.
; в) 10!/2! = 1814400.
Поезду, в котором находится m пассажиров, предстоит сделать n остановок.
а) Сколькими способами могут выйти пассажиры на этих остановках?
б) Решите ту же задачу, если учитывается лишь количество пассажиров, вышедших на каждой остановке.
Решение:
а) nm; б) 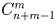 .
.
Задача 40:
В кошельке лежит по 20 монет достоинством в 10, 15 и 20 копеек. Сколькими способами можно из этих 60 монет выбрать двадцать?
Решение:
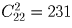 .
.
Задача 41:
Сколькими способами можно расположить в 9 лузах 7 белых и 2 черных шара? Часть луз может быть пустой, а лузы считаются различными.
Решение:
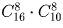 .
.
Задача 42:
Сколькими способами 3 человека могут разделить между собой 6 одинаковых яблок, один апельсин, одну сливу и один мандарин?
Решение:
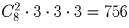 .
.
Задача 43:
Сколькими способами 4 черных шара, 4 белых шара и 4 синих шара можно разложить в 6 различных ящиков?
Решение:
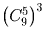 .
.
Задача 44:
Общество из n членов выбирает из своего состава одного представителя.
а) Сколькими способами может произойти открытое голосование, если каждый голосует за одного человека (быть может, и за себя)?
б) Решите ту же задачу, если голосование – тайное, т.е. учитывается лишь число голосов, поданных за каждого кандидата, и не учитывается, кто за кого голосовал персонально.
Решение:
а) nn; б) 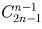 .
.
Сколькими способами можно выложить в ряд 5 красных, 5 синих и 5 зеленых шаров так, чтобы никакие два синих шара не лежали рядом?
Решение:
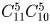 .
.
Сколькими способами можно представить 1000000 в виде произведения трех множителей, если произведения, отличающиеся порядком множителей, считаются различными?
Решение:
1000000 = 26 • 56. Каждый множитель однозначно
определяется количеством двоек и пятерок, входящих в его
разложение. Суммарное количество в трех множителях как двоек,
так и пятерок, равно 6. Ответ: 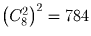 .
.
На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?
Решение:
Рассмотрите 7 оставшихся на полке книг. Между каждыми
двумя соседними (и справа и слева от крайних) либо есть пустое
место (от одной вынутой книги) либо нет. Набор пустых мест
однозначно определяет комплект вынутых книг. Ответ: 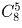 .
.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Комбинаторика-2 >> Шары и перегородки | Убрать решения |