 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Главное неравенство | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Неравенства. Главное неравенство |
|
|
Докажите, что 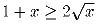 при x ≥ 0.
при x ≥ 0.
Решение:
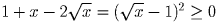 .
.
Докажите, что x + 1/x ≥ 2 при x > 0.
Решение:
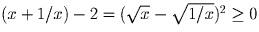 , ч.т.д.
, ч.т.д.
Докажите, что (x² + y²)/2 ≥ xy при любых x и y.
Решение:
Перегруппировав члены, получаем (x – y)² ≥ 0.
Задача 20:Докажите, что 2(x² + y²) ≥ (x + y)² при любых x и y.
Решение:
Перегруппировав члены, получаем (x – y)² ≥ 0.
Задача 21:Докажите, что 1/x + 1/y ≥ 4/(x + y) при x,y > 0.
Решение:Приводим к общему знаменателю и получаем (x – y)² ≥ 0.
Задача 22:
Докажите, что x² + y² + z² ≥ xy + yz + zx при любых x, y, z.
Решение:
Запишем три неравенства:
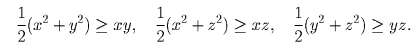
Задача 23:
a, b, c ≥ 0. Докажите, что (a + b)(a + c)(b + c) ≥ 8abc.
Решение:
Надо перемножить три неравенства: 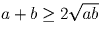 ,
,
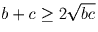 ,
, 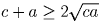 .
.
a, b, c ≥ 0. Докажите, что
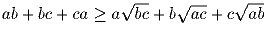 .
.
Решение:
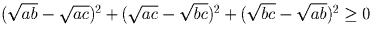 .
.
Докажите, что x² + y² + 1 ≥ xy + x + y при любых x и y.
Решение:
x² + y² + 1 – xy – x – y = ((x – y)² + (x – 1)² + (y – 1)²)/2 ≥ 0.
Задача 26:Докажите, что при любых a, b, c имеет место неравенство: a4 + b4 + c4 ≥ abc(a + b + c).
Решение:
Воспользуемся неравенством x² + y² + z² ≥ xy + yz + zx, причем дважды:
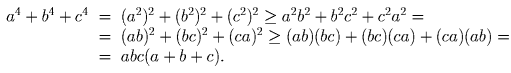
Докажите, что x4 + y4 + 8 ≥ 8xy при любых x и y.
Решение:
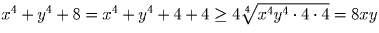 .
.
Задача 28:
a, b, c, d – положительные числа. Докажите, что
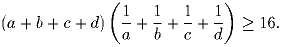
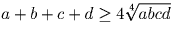 ;
; 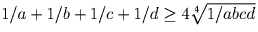 . Осталось лишь перемножить неравенства.
. Осталось лишь перемножить неравенства.
a, b, c – положительные числа. Докажите, что
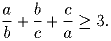
Решение:
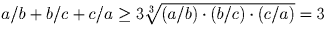 .
.
Докажите, что при x ≥ 0 имеет место неравенство 3x³ – 6x² + 4 ≥ 0.
Решение:
Докажем, что 3x³ + 4 ≥ 6x². Но 3x³ + 4 = 2x³ + x³ + 4. Применяя неравенство Коши, получаем
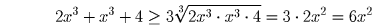
Докажите, что при a, b, c > 0 имеет место неравенство
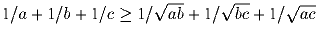 .
.
Задача 32:
Докажите, что при a, b, c > 0 имеет место неравенство ab/c + ac/b + bc/a ≥ a + b + c.
Задача 33:
Докажите, что при a, b, c ≥ 0 имеет место неравенство ((a + b + c)/3)² ≥ (ab + bc + ca)/3.
Задача 34:
Докажите, что при a, b, c ≥ 0 имеет место неравенство (ab + bc + ca)² ≥ 3abc(a + b + c).
Задача 35:
Сумма трех положительных чисел равна шести. Докажите, что сумма их квадратов не меньше 12.
Задача 36:
Докажите, что при x ≥ 0 имеет место неравенство
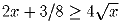 .
.
Задача 37:
Сумма двух неотрицательных чисел равна 10. Какое максимальное и какое минимальное значение может принимать сумма их квадратов?
Задача 38:
Докажите неравенство Коши для пяти чисел, т.е. докажите, что при a, b, c, d, e ≥ 0 имеет место неравенство
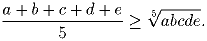
Указание. Докажите сначала неравенство Коши для восьми чисел, а затем воспользуйтесь той же идеей, что и при доказательстве неравенства Коши для трех чисел.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Главное неравенство | Убрать решения |