 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Индукция в неравенствах | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Неравенства. Индукция в неравенствах |
|
|
Докажите, что при n ≥ 3 выполняется неравенство
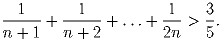
Решение:
База: n = 3. Имеем 1/4 + 1/5 + 1/6 = 37/60 > 3/5. Докажем индукционный переход от n = k к n = k + 1:

Задача 53:
n – натуральное число. Докажите, что
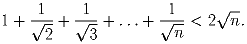
Решение:
База очевидна. Переход:
 , так как
, так как
 .
.
Задача 54:
n – натуральное число. Докажите, что
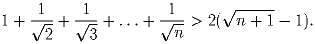
(54) Решение совершенно аналогично предыдущему. Нужно лишь поменять знаки неравенств.
Задача 55:
n – натуральное число. Докажите, что
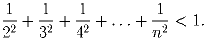
В качестве bn выберем последовательность (1 – 1/n). База: n = 2. 1/2² < 1 – 1/2 – все в порядке.
Индукционный переход (по схеме!): ak – ak – 1 = 1/k², bk – bk – 1 = 1/k(k – 1), т.е. ak – ak – 1 < bk – bk – 1. Отсюда вывод: для любого натурального n имеем an < bn = 1 – 1/n < 1.
Задача 56:(Неравенство Бернулли). x ≥ 0, n – натуральное число. Докажите, что (1 + x)n ≥ 1 + nx.
Решение:

 , ч.т.д.
Задача 57:
, ч.т.д.
Задача 57: n – натуральное число. Докажите, что nn > (n + 1)n – 1.
Решение:
an = nn, bn = (n + 1)n – 1. Проверяем первые значения n = 1, 2 и убеждаемся в том, что для них утверждение задачи верно – это база индукции. Чтобы доказать индукционный переход, достаточно показать, что

n – натуральное число, n ≥ 4. Докажите, что n! ≥ 2n.
Решение:
База n = 4 проверяется непосредственно. Переход: (n + 1)! = (n + 1)n! > 2n(n + 1) > 2 • 2n = 2n + 1.
Задача 59:n – натуральное число. Докажите, что 2n ≥ 2n.
Решение:
База n = 1 очевидна. Переход: 2n + 1 = 2 • 2n > 2 • 2n = 4n > 2(n + 1) (при n > 1).
Задача 60:При каких натуральных n выполняется неравенство 2n ≥ n³?
Решение:
При n ≥ 10.
Задача 61:
Докажите, что для любого натурального n выполняется неравенство 3n > n • 2n.
Задача 62:
Какое из чисел
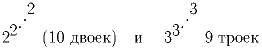
Задача 63:
Произведение положительных чисел a1, a2, …, an равно 1. Докажите, что (1 + a1)(1 + a2) … (1 + an) ≥ 2n. Замечание. У задачи 63 имеются и другие решения, помимо индуктивного.
Задача 64:
Докажите неравенство Бернулли (1 + x)n ≥ 1 + nx, если известно лишь, что x ≥ – 1 и n ≥ 1.
Задача 65:
Сумма положительных чисел x1, x2, …, xn равна 1/2. Докажите, что
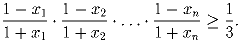
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Индукция в неравенствах | Убрать решения |