 |
 |
|
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Тождественные преобразования | Убрать решения |
|
|
| С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Математический кружок, 2-й год. Неравенства. Тождественные преобразования |
|
|
Решите уравнение a² + b² + c² + d² – ab – bc – cd – d + 2/5 = 0.
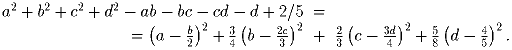
Задача 40:
a + b = 1. Каково максимальное значение величины ab? Указание: a(1 – a) = 1/4 – (1/2 – a)².
Задача 41:
Докажите неравенство (a²/4) + b² + c² ≥ ab – ac + 2bc при любых a, b, c.
Решение:
Разберем решение задачи 41. Переносим все на одну сторону и выделяем квадрат: (a²/4) + b² + c² – ab + ac – 2bc = (a/2 – b + c)² ≥ 0.
Задача 42:k, l, m – натуральные числа. Докажите, что 2k + l + 2k + m + 2l + m ≤ 2k + l + m + 1 + 1.
Решение:
Неравенство доказывается сложением двух очевидных неравенств:

a + b + c = 0. Докажите, что ab + bc + ca ≤ 0.
Решение:ab + bc + ca = ((a + b + c)² – a² – b² – c²)/2 = – (a² + b² + c²)/2 ≤ 0.
Задача 44:Докажите, что x6/y² + y6/x² ≥ x4 + y4 при любых x и y.
Решение:
Обозначим x² = a, y² = b. Тогда

Задача 45:
x, y > 0. Докажите, что
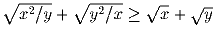 .
.
Решение:
Перенося все члены в одну часть, получаем
 .
.
a, b, c ≥ 0. Докажите, что 2(a³ + b³ + c³) ≥ a²b + ab² + a²c + ac² + b²c + bc².
Решение:
Перенесем все на одну сторону и разобьем слагаемые на четверки: [a³ + b³ – a²b – ab²] + [b³ + c³ – b²c – bc²] + [a³ + c³ – a²c – ac²].
Внутри каждой четверки выражение можно разложить на множители таким образом: a³ + b³ – a²b – ab² = (a – b)(a² – b²) ≥ 0. Отсюда и следует требуемое неравенство.
Задача 47:
a1 ≤ a2 ≤ … ≤ an и b1 ≤ b2 ≤ … ≤ bn. Докажите, что a1b1 + a2b2 + … + anbn ≥ a1c1 + a2c2 + … + ancn, где c1, c2, …, cn – любая перестановка чисел b1, b2, …, bn.
Решение:
Основная идея: если перестановка (ci) не тождественная, то есть номера i и j такие, что ci > cj при i < j. Тогда, поменяв ci и cj местами, мы увеличим сумму произведений. В самом деле, ciai + cjaj – cjai – ciaj = (ai – aj)(ci – cj) < 0. Такими двойными перестановками мы приведем перестановку (ci) к тождественной, в то время как сумма произведений не уменьшится.
Задача 48:
Докажите, что при любом x выполняется неравенство x(x + 1)(x + 2)(x + 3) ≥ – 1.
Задача 49:
Докажите, что при любых x, y, z выполнено неравенство: x4 + y4 + z² + 1 ≥ 2x(xy² – x + z + 1).
Задача 50:
Докажите, что
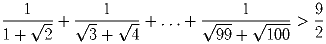
Задача 51:
x, y ≥ 0. Докажите, что 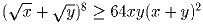 .
.
| Задачная база >> Разное >> Математический кружок. 2-й год >> Неравенства >> Тождественные преобразования | Убрать решения |