Задача 1:
Поставьте вместо звездочек различные цифры от 0 до 9 так,
чтобы сумма дробей
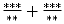
равнялась
а) как можно большему числу;
б) как можно меньшему числу.
Задача 2:
Назовем слово монокоренным, если в нем есть ровно один корень
(слово «монокоренной», например, к монокоренным не относится).
Найдите как можно более длинное монокоренное нарицательное существительное
русского языка (длина вычисляется в именительном падеже единственного
числа).
Задача 3:
Найдите как можно большее натуральное
число, в записи которого не встречается цифра 0, которое делится на сумму
своих цифр, причём любое число, получаемое из него отбрасыванием одной или
нескольких последних цифр, обладает тем же свойством.
Задача 4:
За один ход можно поменять местами либо две соседние
буквы, либо две буквы, стоящие через одну. Преобразовать слово АПЕЛЬСИН в
слово СПАНИЕЛЬ за как можно меньшее число ходов.
Задача 5:
Найдите как можно больше решений ребуса ТРОС + СТАР = КРУПА.
Задача 6:
Расставить на шахматной доске как можно меньше коней так, чтобы
они били все черные поля.
Задача 7:
Получить число 2000 с помощью как можно меньшего количества одинаковых
цифр (допускаются 4 арифметических действия и скобки).
Задача 8:
На листе бумаги отмечены несколько точек так, что для каждой из них
ровно n из отмеченных точек лежит на расстоянии 1. Нарисуйте такую
картинку для как можно большего n.
Задача 9:
Разбейте прямоугольник 1 × 3 на возможно меньшее
число квадратов так, чтобы среди них не нашлось трёх равных.
Задача 10:
Придумайте как можно более длинную цепочку различных слов
(существительных, единственного числа, именительного падежа, не имен
собственных) так, чтобы первые три буквы очередного слова совпадали с
последними тремя буквами предыдущего, например корОЛЬ - ОЛЬха.
Задача 11:
Расставьте на шахматной доске как можно большее число ладей так,
чтобы каждая била нечётное число других.
Задача 12:
Нарисуйте как можно больше прямоугольников, ни один из которых
нельзя покрыть всеми остальными вместе.


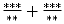 равнялась
а) как можно большему числу;
б) как можно меньшему числу.
Задача 2:
Назовем слово монокоренным, если в нем есть ровно один корень
(слово «монокоренной», например, к монокоренным не относится).
Найдите как можно более длинное монокоренное нарицательное существительное
русского языка (длина вычисляется в именительном падеже единственного
числа).
Задача 3:
Найдите как можно большее натуральное
число, в записи которого не встречается цифра 0, которое делится на сумму
своих цифр, причём любое число, получаемое из него отбрасыванием одной или
нескольких последних цифр, обладает тем же свойством.
Задача 4:
За один ход можно поменять местами либо две соседние
буквы, либо две буквы, стоящие через одну. Преобразовать слово АПЕЛЬСИН в
слово СПАНИЕЛЬ за как можно меньшее число ходов.
Задача 5:
Найдите как можно больше решений ребуса ТРОС + СТАР = КРУПА.
Задача 6:
Расставить на шахматной доске как можно меньше коней так, чтобы
они били все черные поля.
Задача 7:
Получить число 2000 с помощью как можно меньшего количества одинаковых
цифр (допускаются 4 арифметических действия и скобки).
Задача 8:
На листе бумаги отмечены несколько точек так, что для каждой из них
ровно n из отмеченных точек лежит на расстоянии 1. Нарисуйте такую
картинку для как можно большего n.
Задача 9:
Разбейте прямоугольник 1 × 3 на возможно меньшее
число квадратов так, чтобы среди них не нашлось трёх равных.
Задача 10:
Придумайте как можно более длинную цепочку различных слов
(существительных, единственного числа, именительного падежа, не имен
собственных) так, чтобы первые три буквы очередного слова совпадали с
последними тремя буквами предыдущего, например корОЛЬ - ОЛЬха.
Задача 11:
Расставьте на шахматной доске как можно большее число ладей так,
чтобы каждая била нечётное число других.
Задача 12:
Нарисуйте как можно больше прямоугольников, ни один из которых
нельзя покрыть всеми остальными вместе.
равнялась
а) как можно большему числу;
б) как можно меньшему числу.
Задача 2:
Назовем слово монокоренным, если в нем есть ровно один корень
(слово «монокоренной», например, к монокоренным не относится).
Найдите как можно более длинное монокоренное нарицательное существительное
русского языка (длина вычисляется в именительном падеже единственного
числа).
Задача 3:
Найдите как можно большее натуральное
число, в записи которого не встречается цифра 0, которое делится на сумму
своих цифр, причём любое число, получаемое из него отбрасыванием одной или
нескольких последних цифр, обладает тем же свойством.
Задача 4:
За один ход можно поменять местами либо две соседние
буквы, либо две буквы, стоящие через одну. Преобразовать слово АПЕЛЬСИН в
слово СПАНИЕЛЬ за как можно меньшее число ходов.
Задача 5:
Найдите как можно больше решений ребуса ТРОС + СТАР = КРУПА.
Задача 6:
Расставить на шахматной доске как можно меньше коней так, чтобы
они били все черные поля.
Задача 7:
Получить число 2000 с помощью как можно меньшего количества одинаковых
цифр (допускаются 4 арифметических действия и скобки).
Задача 8:
На листе бумаги отмечены несколько точек так, что для каждой из них
ровно n из отмеченных точек лежит на расстоянии 1. Нарисуйте такую
картинку для как можно большего n.
Задача 9:
Разбейте прямоугольник 1 × 3 на возможно меньшее
число квадратов так, чтобы среди них не нашлось трёх равных.
Задача 10:
Придумайте как можно более длинную цепочку различных слов
(существительных, единственного числа, именительного падежа, не имен
собственных) так, чтобы первые три буквы очередного слова совпадали с
последними тремя буквами предыдущего, например корОЛЬ - ОЛЬха.
Задача 11:
Расставьте на шахматной доске как можно большее число ладей так,
чтобы каждая била нечётное число других.
Задача 12:
Нарисуйте как можно больше прямоугольников, ни один из которых
нельзя покрыть всеми остальными вместе.