 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Делимость-1 | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2000 г, 6 класс. Делимость-1 |
|
|
Задача 4: Доказать а) если сумма любых двух из трёх чисел делится на 3, то и сумма всех трёх чисел делится на 3; б) если сумма любых трёх из четырёх чисел делится на 4, то и каждое число делится на 4; в) сформулируйте и докажите утверждение б) для n чисел. Задача 5: Докажите, что число, составленное из пятидесяти пяти единиц, является составным. Задача 6: На новом супер-калькуляторе есть только три кнопки: «умножить на 7», «прибавить 27» и «вычесть 12". Можно ли на этом калькуляторе из числа 6 получить число 1? Какие числа можно получить из числа 6? Задача 7: Докажите, что числа вида
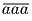 делятся и на 3 и на 37.
Задача 8:
Петя и Вася задумали по трёхзначному числу, затем каждый приписал к
нему такое же число. У полученного шестизначного числа они выписали все
натуральные делители. Докажите, что не менее 8 чисел в их списках совпало.
Задача 9:
Делится ли число 77…77 (666 семерок) на 13?
Задача 10:
При каких n число 88…88 (n восмерок) делится на 91?
Задача 11:
Дана полоска из 6 клеток. Петя и Вася по очереди записывают в клетки
цифры. Если полученное число делится на 91, то выигрывает Вася, если нет, то
Петя. Всегда ли Вася сможет победить? А если полоска состоит из 12 клеток?
Задача 12:
У царя Дадона в одиночных камерах сидели 100 пленников. Поворот ручки
отпирает каждую камеру, следующий поворот запирает, еще один снова отпирает
и т.д. К празднику царь решил освободить часть пленников и накануне послал
слугу, который повернул ручку на дверях каждой камеры. Все двери оказались
отперты. Но тут пришел второй посыльный и повернул ручку каждой второй
камеры. Двери камер 2, 4, 6, … вновь оказались заперты.
Следующий посланец повернул ручки камер 3, 6, 9, 12 и т.д. Еще
один – в каждой четвертой камере. То же повторяли следующие посланцы вплоть
до сотого, повернувшего ручку сотой камеры. Наконец наступил праздник, и
сидевшие в открытых камерах вышли на свободу. Сколько пленников освободил
Дадон?
делятся и на 3 и на 37.
Задача 8:
Петя и Вася задумали по трёхзначному числу, затем каждый приписал к
нему такое же число. У полученного шестизначного числа они выписали все
натуральные делители. Докажите, что не менее 8 чисел в их списках совпало.
Задача 9:
Делится ли число 77…77 (666 семерок) на 13?
Задача 10:
При каких n число 88…88 (n восмерок) делится на 91?
Задача 11:
Дана полоска из 6 клеток. Петя и Вася по очереди записывают в клетки
цифры. Если полученное число делится на 91, то выигрывает Вася, если нет, то
Петя. Всегда ли Вася сможет победить? А если полоска состоит из 12 клеток?
Задача 12:
У царя Дадона в одиночных камерах сидели 100 пленников. Поворот ручки
отпирает каждую камеру, следующий поворот запирает, еще один снова отпирает
и т.д. К празднику царь решил освободить часть пленников и накануне послал
слугу, который повернул ручку на дверях каждой камеры. Все двери оказались
отперты. Но тут пришел второй посыльный и повернул ручку каждой второй
камеры. Двери камер 2, 4, 6, … вновь оказались заперты.
Следующий посланец повернул ручки камер 3, 6, 9, 12 и т.д. Еще
один – в каждой четвертой камере. То же повторяли следующие посланцы вплоть
до сотого, повернувшего ручку сотой камеры. Наконец наступил праздник, и
сидевшие в открытых камерах вышли на свободу. Сколько пленников освободил
Дадон?Задача 13: Делится ли 29 × 3 на 2? А на 5? На 6? Делится ли 2² × 3³ × 55 на 120? Задача 14: Число a не делится на 3. Может ли делится на 3 число 2a? Задача 15: Число a чётно. Верно ли, что число 3a делится на 6? Задача 16: Число 5a делится на 3. Верно ли, что a делится на 3? Задача 17: Если число a делится на 3 и на 4, то следует ли отсюда, что оно делится и на 12? А если a делится на 4 и на 6, то следует ли отсюда, что оно делится на 24? Задача 18: Число 15a делится на 6. Верно ли что a тоже делится на 6?
Взаимно простые числа. Обобщить результат задач 5 и 6: если a делится на m и на n, m и n взаимно просты, то a делится на mn; если ap делится на q, p и q взаимно просты, то a делится на q.
Задача 19: Известно, что a + 15 делится на 5. Делится ли a на 5? Задача 20: Если число a делится на 3 и b делится на 3, верно ли, что тогда сумма a и b делится на 3? А разность a и b? Задача 21: Вспомнить некоторые свойства делимости:а) 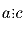 и
и 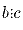 , то
, то 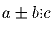 .
.
б) 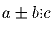 , и
, и 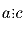 , то и
, то и 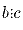 .
.
в) 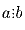 и
и 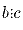 , то и
, то и 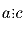 .
.
Задача 26: Разложите на простые множители 2000, 2001, 1999. Задача 27: Сколько делителей у числа 25 × 3³ × 5²? А у чисел 2000, 2001, 1999? Задача 28: Сколько делителей у чисел 1, 4, 9, 16, 25; а у чисел 5, 10, 15, 24? Сравните количество делителей.
Задача 29: Может ли в разложении числа n² на простые множители содержаться ровно 5 «троек»?
Задача 30: Делится ли 11! + 12! на 13? Задача 31: На сколько нулей заканчивается 200!,? Задача 32: Может ли n! оканчиваться ровно на 5 нулей? Задача 33: Каково наименьшее натуральное n такое, что n! делится на 1999, 2000, 2001?
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Делимость-1 | Убрать решения |