Задача 1:
Существует ли такая тройка натуральных чисел, что
любые два из них имеют общий делитель, больший единицы,
но общим делителем для всех трёх чисел является только 1?
Задача 2:
Можно ли монетами в 14 и 35 шиллингов заплатить без сдачи сумму в
1999 шиллингов?
Решение:
Нельзя, так как 1999 не кратно НОД(14,35).
Задача 3:
В банк можно положить за один раз 120 руб. или снять 300 руб.
У кого-то есть 1000 руб. Какую наибольшую сумму кто-то
может положить в банк за несколько раз?
Решение:
960. Оценка получается из делимости. Снять и положить можно только
числа, делящиеся на 60 (120 = 60 × 2, 300 = 60 × 5), максимальное
число, меньшее 1000 и делящееся на 60 – это 960. Пример: кладём 3
раза по 300, снимаем 2 раза по 120 и кладём
300.
Задача 4:
a = 2³ • 3¹º • 5 • 7² , b = 2
5 • 3 • 11. Чему
равен НОД (a,b)?
Решение:
НОД – это общая часть разложений.
Задача 5:
a = 2
8 • 5³ • 7 , b = 2
5 • 3 • 5
7. Чему
равен
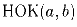
?
Решение:
НОК – это объединение разложений.
Задача 6:
Про натуральные числа a и b известно, что 15a = 14b и что
НОД (a,b) = 13. Найдите a и b.
Задача 7:
Докажите, что для любых натуральных чисел a и b верно равенство
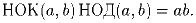
Задача 8:
Докажите, что если a и b – натуральные числа (a > b),
то НОД (a,b) = НОД (a – b,b)
Задача 9:
Может ли наименьшее общее кратное двух натуральных чисел равняться их
сумме?
Решение:
Пусть такие числа x и y существуют.
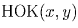
делится на
x и на y. Тогда x + y делится на x и на y, значит, x
делится на y и
y делится на x, поэтому x = y. Но тогда
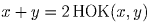
, что
противоречит предположению.
Задача 10:
Может ли наименьшее общее кратное трёх чисел равняться их сумме?
Решение:
Да, например, 6 = 1 + 2 + 3.
Задача 11:
НОД двух натуральных чисел в восемь раз меньше, чем их
НОК. Докажите, что одно из этих чисел делится на другое.
Задача 12:
Даны 6 натуральных чисел. Могут ли среди их попарных
НОДов встречаться все натуральные числа от 1 до 15?
Решение:
Нет. Так как какие-то числа имеют НОДы, равные 7 и 14,
то есть не менее трёх чисел, кратных 7. Но тогда существует
третий НОД, кратный 7, а среди чисел от 1 до 15 такого нет.
(Аналогичное рассуждение проходит по делимости на 2).
Задача 13:
Разность двух нечётных чисел является степенью двойки.
Докажите, что они взаимно просты.
Решение:
НОД (a,b) = НОД (a,a – b) = НОД (a,2
k).
Задача 14:
Известно, что (n – 1)! + 1 делится на n.
Докажите, что число n – простое.
Решение:
Если n – составное, то (n – 1)! делится на n.
Задача 15:
В результате некоторой перестановки цифр число уменьшилось в три раза.
Докажите, что исходное число делилось на 27.
Задача 16:
Найдите все такие
натуральные a, что число а)
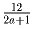
;
б)
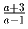
; в)
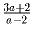
– тоже целое.


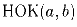 ?
Решение:
НОК – это объединение разложений.
Задача 6:
Про натуральные числа a и b известно, что 15a = 14b и что
НОД (a,b) = 13. Найдите a и b.
Задача 7:
Докажите, что для любых натуральных чисел a и b верно равенство
?
Решение:
НОК – это объединение разложений.
Задача 6:
Про натуральные числа a и b известно, что 15a = 14b и что
НОД (a,b) = 13. Найдите a и b.
Задача 7:
Докажите, что для любых натуральных чисел a и b верно равенство
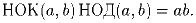
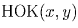 делится на
x и на y. Тогда x + y делится на x и на y, значит, x
делится на y и
y делится на x, поэтому x = y. Но тогда
делится на
x и на y. Тогда x + y делится на x и на y, значит, x
делится на y и
y делится на x, поэтому x = y. Но тогда 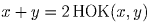 , что
противоречит предположению.
Задача 10:
Может ли наименьшее общее кратное трёх чисел равняться их сумме?
Решение:
Да, например, 6 = 1 + 2 + 3.
Задача 11:
НОД двух натуральных чисел в восемь раз меньше, чем их
НОК. Докажите, что одно из этих чисел делится на другое.
Задача 12:
Даны 6 натуральных чисел. Могут ли среди их попарных
НОДов встречаться все натуральные числа от 1 до 15?
Решение:
Нет. Так как какие-то числа имеют НОДы, равные 7 и 14,
то есть не менее трёх чисел, кратных 7. Но тогда существует
третий НОД, кратный 7, а среди чисел от 1 до 15 такого нет.
(Аналогичное рассуждение проходит по делимости на 2).
Задача 13:
Разность двух нечётных чисел является степенью двойки.
Докажите, что они взаимно просты.
Решение:
НОД (a,b) = НОД (a,a – b) = НОД (a,2k).
Задача 14:
Известно, что (n – 1)! + 1 делится на n.
Докажите, что число n – простое.
Решение:
Если n – составное, то (n – 1)! делится на n.
Задача 15:
В результате некоторой перестановки цифр число уменьшилось в три раза.
Докажите, что исходное число делилось на 27.
Задача 16:
Найдите все такие
натуральные a, что число а)
, что
противоречит предположению.
Задача 10:
Может ли наименьшее общее кратное трёх чисел равняться их сумме?
Решение:
Да, например, 6 = 1 + 2 + 3.
Задача 11:
НОД двух натуральных чисел в восемь раз меньше, чем их
НОК. Докажите, что одно из этих чисел делится на другое.
Задача 12:
Даны 6 натуральных чисел. Могут ли среди их попарных
НОДов встречаться все натуральные числа от 1 до 15?
Решение:
Нет. Так как какие-то числа имеют НОДы, равные 7 и 14,
то есть не менее трёх чисел, кратных 7. Но тогда существует
третий НОД, кратный 7, а среди чисел от 1 до 15 такого нет.
(Аналогичное рассуждение проходит по делимости на 2).
Задача 13:
Разность двух нечётных чисел является степенью двойки.
Докажите, что они взаимно просты.
Решение:
НОД (a,b) = НОД (a,a – b) = НОД (a,2k).
Задача 14:
Известно, что (n – 1)! + 1 делится на n.
Докажите, что число n – простое.
Решение:
Если n – составное, то (n – 1)! делится на n.
Задача 15:
В результате некоторой перестановки цифр число уменьшилось в три раза.
Докажите, что исходное число делилось на 27.
Задача 16:
Найдите все такие
натуральные a, что число а) 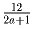 ;
б)
;
б) 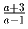 ; в)
; в) 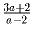 – тоже целое.
– тоже целое.