Задача 1:
В квадратном ковре со стороной 1 м моль проела 51 дырку
(дырка – точка). Докажите, что некоторой квадратной заплаткой
со стороной 50 см можно закрыть не менее 13 дырок.
Решение:
Разобьём ковёр на 4 квадрата 50 см × 50 см.
В один из них обязательно попадёт 13 дырок. На него и наложим
заплатку.
Задача 2:
В квадратном ковре со стороной 1 м моль проела 51 дырку
(дырка – точка). Докажите, что некоторой квадратной заплаткой со
стороной 20 см можно закрыть не менее трёх дырок.
Решение:
Разобьём ковёр на 25 квадратов 20 см × 20 см.
В один из них обязательно попадёт 3 точки. На него и наложим
заплатку.
Задача 3:
В квадратном ковре со стороной 1 м моль проела 15 дырок.
Докажите, что из этого ковра можно вырезать круг
радиуса 12.5 см, в котором нет ни одной дырки.
Решение:
Разобьём ковёр на 16 квадратов 25 см × 25 см.
В одном из них не будет ни одной дырки, значит, из него можно вырезать
круг без дырок.
Задача 4:
Какое наибольшее число клеток можно закрасить на шахматной доске
8 × 8 так, чтобы в любом уголке из трёх клеток

были
как закрашенные, так и незакрашенные клетки?
Решение:
Разобьём доску на 16 квадратов 2 × 2. В каждом из них должно
быть ровно две закрашенные клетки (иначе найдётся одноцветный уголок).
Значит закрашенных клеток должно быть 16 • 2 = 32. Примеры –
раскраска «зеброй» или стандартная шахматная раскраска.
Задача 5:
На шахматной доске стоит 31 фишка. Докажите, что найдется
свободный уголок из трёх клеток

.
Решение:
Разобьём доску на 16 квадратов 2 × 2. В одном из них
не более одной фишки, значит в нём найдётся свободный уголок.
Задача 6:
В правильном 20-угольнике отметили 9 вершин. Докажите, что
найдется равнобедренный треугольник с вершинами в отмеченных точках.
Решение:
Разобьём вершины 20-угольника на 4 группы так, чтобы
вершины, входящие в каждую из них, образовывали правильный
пятиугольник. По принципу Дирихле какие-то 3 (
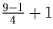
)
из отмеченных вершин попадут в одну группу. Остаётся заметить, что
любые три вершины правильного пятиугольника образуют равнобедренный
треугольник.
Задача 7:
Прямая раскрашена в два цвета. Докажите, что существует отрезок,
оба конца и середина которого окрашены в один цвет.
Решение:
Пусть такого отрезка нет. Возьмём отрезок AB с концами
одного (синего) цвета.
Теперь возьмём на прямой по разные стороны от отрезка точки D и E
так, чтобы расстояние от них до концов отрезка AB равнялось его
длине
(DA = AB = BE). Они, очевидно, должны быть несинего (красного) цвета.
Середина отрезака DE, стало быть, должна быть синей. Но она также
является серединой отрезка AB, у которого синие концы.
Задача 8:
Плоскость раскрашена в два цвета. Докажите, что на ней найдется
правильный треугольник с одноцветными вершинами.
Решение:
Рассмотрим три синие точки A, B и C, такие, что
B – середина отрезка AC (они существуют согласно
предыдущей задаче). Пусть D – третья вершина правильного
треугольника ACD, E и F – третьи вершины правильных
треугольников ABE и BFC, лежащие в той же полуплоскости
(относительно AC), что и точка D. Тогда либо хотя бы одна
из точек D, E и F окрашена в синий цвет (и тогда образуется синий
правильный треугольник), либо все эти три точки красные и
образуют красный правильный треугольник.
Задача 9:
Доска 6 × 6 заполнена костяшками домино 1 × 2.
Докажите, что можно провести вертикальный или горизонтальный разрез
доски, не пересекающий ни одной из костяшек.
Решение:
Каждая строка, очевидно, пересекает чётное число вертикальных
доминошек. Первый (верхний) возможный горизонтальный разрез по
линии сетки пересекает ровно те доминошки, которые пересекает первая строка,
то есть чётное число. Второй разрез – те, что занимает вторая строка, кроме
тех, которые пересекает первый разрез – тоже чётное число. Рассуждая
далее, выясняем, что каждый горизонтальный разрез пересекает чётное число
доминошек. Аналогично доказывается, что каждый вертикальный разрез
пересекает чётное число доминошек.
Таким образом, если требуемого разреза провести нельзя, то каждый
из 10 возможных разрезов по линии сетки пересекает как минимум 2 доминошки,
значит все они пересекают как минимум 20 доминошек. Но в разбиении доски
участвуют только 18 доминошек.
Задача 10:
Клетки прямоугольника 5 × 41 раскрашены в два цвета.
Докажите, что можно выбрать три строки и три столбца так, что все 9
клеток, находящихся на их пересечении, будут иметь один цвет.
Решение:
Найдётся хотя бы 21 столбец, в котором будет преобладать
один из цветов (назовём этот цвет чёрным, а другой цвет –
белым). Если в каком-нибудь из этих столбцов больше трёх чёрных клеток –
перекрасим некоторые клетки в белый цвет так, чтобы в каждом из 21 столбца
было три чёрных клетки.
Теперь заметим, что вариантов расстановки этих трёх чёрных клеток в столбце
всего 10, а, значит, раскраска хотя бы трёх столбцов совпадает.
Задача 11:
Какое наибольшее число королей можно поставить на шахматной
доске так, чтобы они не били друг друга?
Решение:
16.
Пример расстановки 16 королей несложен –
королей надо поставить «горошком». Теперь докажем, что больше 16
королей не поставить. Разобьём доску на 16 квадратов 2 × 2.
Если короли не бьют друг друга, то в каждом квадратике должно быть не
более одного короля, значит, всего королей не более 16.


 были
как закрашенные, так и незакрашенные клетки?
Решение:
Разобьём доску на 16 квадратов 2 × 2. В каждом из них должно
быть ровно две закрашенные клетки (иначе найдётся одноцветный уголок).
Значит закрашенных клеток должно быть 16 • 2 = 32. Примеры –
раскраска «зеброй» или стандартная шахматная раскраска.
Задача 5:
На шахматной доске стоит 31 фишка. Докажите, что найдется
свободный уголок из трёх клеток
были
как закрашенные, так и незакрашенные клетки?
Решение:
Разобьём доску на 16 квадратов 2 × 2. В каждом из них должно
быть ровно две закрашенные клетки (иначе найдётся одноцветный уголок).
Значит закрашенных клеток должно быть 16 • 2 = 32. Примеры –
раскраска «зеброй» или стандартная шахматная раскраска.
Задача 5:
На шахматной доске стоит 31 фишка. Докажите, что найдется
свободный уголок из трёх клеток  .
Решение:
Разобьём доску на 16 квадратов 2 × 2. В одном из них
не более одной фишки, значит в нём найдётся свободный уголок.
Задача 6:
В правильном 20-угольнике отметили 9 вершин. Докажите, что
найдется равнобедренный треугольник с вершинами в отмеченных точках.
Решение:
Разобьём вершины 20-угольника на 4 группы так, чтобы
вершины, входящие в каждую из них, образовывали правильный
пятиугольник. По принципу Дирихле какие-то 3 (
.
Решение:
Разобьём доску на 16 квадратов 2 × 2. В одном из них
не более одной фишки, значит в нём найдётся свободный уголок.
Задача 6:
В правильном 20-угольнике отметили 9 вершин. Докажите, что
найдется равнобедренный треугольник с вершинами в отмеченных точках.
Решение:
Разобьём вершины 20-угольника на 4 группы так, чтобы
вершины, входящие в каждую из них, образовывали правильный
пятиугольник. По принципу Дирихле какие-то 3 (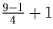 )
из отмеченных вершин попадут в одну группу. Остаётся заметить, что
любые три вершины правильного пятиугольника образуют равнобедренный
треугольник.
Задача 7:
Прямая раскрашена в два цвета. Докажите, что существует отрезок,
оба конца и середина которого окрашены в один цвет.
Решение:
Пусть такого отрезка нет. Возьмём отрезок AB с концами
одного (синего) цвета.
Теперь возьмём на прямой по разные стороны от отрезка точки D и E
так, чтобы расстояние от них до концов отрезка AB равнялось его
длине
(DA = AB = BE). Они, очевидно, должны быть несинего (красного) цвета.
Середина отрезака DE, стало быть, должна быть синей. Но она также
является серединой отрезка AB, у которого синие концы.
Задача 8:
Плоскость раскрашена в два цвета. Докажите, что на ней найдется
правильный треугольник с одноцветными вершинами.
Решение:
Рассмотрим три синие точки A, B и C, такие, что
B – середина отрезка AC (они существуют согласно
предыдущей задаче). Пусть D – третья вершина правильного
треугольника ACD, E и F – третьи вершины правильных
треугольников ABE и BFC, лежащие в той же полуплоскости
(относительно AC), что и точка D. Тогда либо хотя бы одна
из точек D, E и F окрашена в синий цвет (и тогда образуется синий
правильный треугольник), либо все эти три точки красные и
образуют красный правильный треугольник.
Задача 9:
Доска 6 × 6 заполнена костяшками домино 1 × 2.
Докажите, что можно провести вертикальный или горизонтальный разрез
доски, не пересекающий ни одной из костяшек.
Решение:
Каждая строка, очевидно, пересекает чётное число вертикальных
доминошек. Первый (верхний) возможный горизонтальный разрез по
линии сетки пересекает ровно те доминошки, которые пересекает первая строка,
то есть чётное число. Второй разрез – те, что занимает вторая строка, кроме
тех, которые пересекает первый разрез – тоже чётное число. Рассуждая
далее, выясняем, что каждый горизонтальный разрез пересекает чётное число
доминошек. Аналогично доказывается, что каждый вертикальный разрез
пересекает чётное число доминошек.
)
из отмеченных вершин попадут в одну группу. Остаётся заметить, что
любые три вершины правильного пятиугольника образуют равнобедренный
треугольник.
Задача 7:
Прямая раскрашена в два цвета. Докажите, что существует отрезок,
оба конца и середина которого окрашены в один цвет.
Решение:
Пусть такого отрезка нет. Возьмём отрезок AB с концами
одного (синего) цвета.
Теперь возьмём на прямой по разные стороны от отрезка точки D и E
так, чтобы расстояние от них до концов отрезка AB равнялось его
длине
(DA = AB = BE). Они, очевидно, должны быть несинего (красного) цвета.
Середина отрезака DE, стало быть, должна быть синей. Но она также
является серединой отрезка AB, у которого синие концы.
Задача 8:
Плоскость раскрашена в два цвета. Докажите, что на ней найдется
правильный треугольник с одноцветными вершинами.
Решение:
Рассмотрим три синие точки A, B и C, такие, что
B – середина отрезка AC (они существуют согласно
предыдущей задаче). Пусть D – третья вершина правильного
треугольника ACD, E и F – третьи вершины правильных
треугольников ABE и BFC, лежащие в той же полуплоскости
(относительно AC), что и точка D. Тогда либо хотя бы одна
из точек D, E и F окрашена в синий цвет (и тогда образуется синий
правильный треугольник), либо все эти три точки красные и
образуют красный правильный треугольник.
Задача 9:
Доска 6 × 6 заполнена костяшками домино 1 × 2.
Докажите, что можно провести вертикальный или горизонтальный разрез
доски, не пересекающий ни одной из костяшек.
Решение:
Каждая строка, очевидно, пересекает чётное число вертикальных
доминошек. Первый (верхний) возможный горизонтальный разрез по
линии сетки пересекает ровно те доминошки, которые пересекает первая строка,
то есть чётное число. Второй разрез – те, что занимает вторая строка, кроме
тех, которые пересекает первый разрез – тоже чётное число. Рассуждая
далее, выясняем, что каждый горизонтальный разрез пересекает чётное число
доминошек. Аналогично доказывается, что каждый вертикальный разрез
пересекает чётное число доминошек.