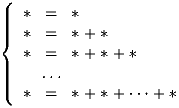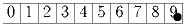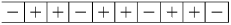Задача 1: Игра начинается с числа 60. За ход разрешается уменьшить имеющееся число на любой из его делителей. Проигрывает тот, кто получит ноль.

Решение: Во-первых, заметим, что эта игра всегда заканчивается победой одного из игроков: числа на доске постоянно уменьшаются, поэтому рано или поздно на доске окажется число 0. Теперь докажем, что выигрывает первый. Своим ходом он всегда может забирать 1, оставляя второму нечётное число. Второй должен отнять от нечётного числа какой-нибудь его делитель, а поскольку все делители нечётных чисел нечётны, то в результате после хода второго на доске опять окажется чётное число. Таким образом, первый игрок всегда сможет сделать ход, то есть он не может проиграть. Следовательно (см. первое замечание), проиграет второй.

Задача 2: Волк и Заяц играют в следующую игру: на доске написано некоторое натуральное число с ненулевой последней цифрой. Ход состоит в том, что из числа вычитают какую-нибудь его ненулевую цифру и пишут результат вместо старого числа. Выигрывает тот, кто первым получит нуль.

Решение: Первый игрок постоянно вычитает из числа его последнюю (ненулевую!) цифру.

Задача 3: Имеется две кучи конфет: в первой – 40, во второй – 45. За ход нужно одну кучу съесть, а другую разделить на две (не обязательно равные). Проигрывает тот, кто не может сделать ход.

Решение: В этой игре выигрывает первый игрок. Он всегда съедает нечётную кучку, а чётную делит на две нечётных – в результате после его хода оказываются две нечётных кучки, а после хода второго – снова одна нечётная и одна чётная кучка. Единственная позиция, в которой невозможно сделать ход – позиция (1,1), которая могла получиться только после хода первого игрока.

Задача 4: Имеется две кучи конфет: в первой – 100, во второй – 201. За ход разрешается съесть из одной кучки любое число конфет, являющееся делителем количества конфет в другой кучке. Выигрывает тот, кто съедает последнюю конфету.

Решение: И здесь выигрышными являются позиции, в которых обе кучки содержат нечётное число конфет. Первый игрок должен своим ходом взять 1 конфету из первой кучки.

Задача 5: Два игрока ставят по очереди числа вместо звездочек в следующей системе равенств:

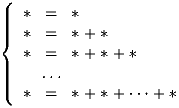
(в последнем равенстве справа 8 слагаемых). Второй игрок выигрывает, если все равенства выполняются, в противном случае выигрывает первый.

Решение: Эта задача кодируется игрой про 8 шашек, стоящих на диагонали шахматной доски.

Задача 6: Имеется полоска клетчатой бумаги длиной 10 клеток. В крайней правой ее клетке стоит шашка (рис. 1). Двое играющих по очереди передвигают ее влево на одну или две клетки. Проигрывает тот, кому некуда ходить.

6cm

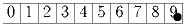
Рис 1.

Решение: Представим себе, что шашка уже дошла до крайней левой клетки, помеченной на рис. 1 цифрой 0. Понятно, что в этом случае проиграл тот, чья очередь ходить (назовем его очередником), потому что ходить ему некуда. А вот если шашка стоит на клетках 1 или 2 то очередник одним ходом сдвинет ее на клетку 0 и выиграет. Отметим клетку 0, где очередником быть невыгодно, минусом, а выгодные для очередника клетки 1 и 2 – плюсами (рис. 2).

6cm

Рис 2.

6cm

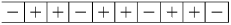
Рис 3.

Теперь посмотрим, каково быть очередником, когда шашка стоит на клетке 3? Если сдвинуть шашку на одну клетку, она окажется на клетке 2, а если на две – на клетке 1. Обе клетки выгодны для очередника, да только очередником будет уже не тот, кто ходил, а его партнер. Он и выиграет. Получается, что клетка 3 для очередника невыгодна, а клетки 4 и 5 выгодны: с них очередник одним ходом переводит шашку на клетку 3, и его партнер, став очередником, оказывается у разбитого корыта. Продолжая в том же духе, нетрудно показать, что клетка 6 невыгодна для очередника, клетки 7 и 8 – выгодны, а клетка 9 – снова невыгодна (рис. 3). Стало быть выигрывает второй игрок.

Задача 7: Кто выигрывает в игре Баше, если длина полоски составляет 11 клеток? 12 клеток? 13 клеток? 2000 клеток?

Решение: Как видно из решения предыдущей задачи, невыгодные для очередника позиции – это клетки, номера которых имеют остаток 1 при делении на 3. Поэтому на полоске длиной 12 клеток выигрывает второй игрок, а на полосках длин 11, 13 и 2000 клеток – первый.

Задача 8: Изменим правила игры Баше: теперь за один ход можно сдвигать шашку на 1, 2, 3, 4 или 5 клеток, а длина полоски – 13 клеток.

Решение: Нарисуем эту полоску и, как в предыдущей задаче, отметим на ней плюсами и минусами клетки, выгодные и невыгодные для очередника. Получается, что невыгодные для очередника клетки (то есть клетки, на которые надо ходить, чтобы выиграть) имеют остаток 1 при делении на 6.

Задача 9: А теперь в игре Баше можно сдвигать шашку на 3, 6, 9 или 12 клеток, а длина полоски – 40 клеток.

Задача 10: Проанализируйте игру Баше, где можно сдвигать шашку на 1, 3 или 4 клетки, а длина полоски – 15 клеток. А что можно сказать про случай, если длина полоски – 2000 клеток?