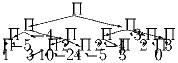Задача 1: Имеется 40 конфет. Двое по очереди едят от одной до шести из них. Выигрывает съевший последнюю конфету.

Решение: А что это, как не игра Баше? Первым ходом нужно съесть 5 конфет.

Задача 2: Имеется 40 конфет. Двое по очереди едят от 1 до 6 из них. Тот, кто съел последнюю, проигрывает.

Решение: Это тоже игра Баше, только цель в ней – достичь не нуля конфет, а одной конфеты! Все выигрышные позиции сдвинуты на 1 относительно «стандартной» игры. Первый игрок должен первым ходом съесть 4 конфеты.

Задача 3: В 6-й класс ЛМШ приехало 50 школьников. За ход разрешается съесть двух, четверых или семерых из них. Проигрывает тот, кто не может сделать ход.

Решение: Выигрышными здесь являются все «позиции», в которых число школьников больше 3 и не кратно 3, а также «позиции» 2 и 3. Работает стратегия «ставь на минус!» – первым ходом игрок должен съесть двух школьников и оставить 48. Затем на каждый ход 2 он отвечает ходом 7, а на каждый ход 4 или 7 – ходом 2. Так он действует до тех пор, пока число школьников не станет равно 6, 9 или 12. В позиции «12» на ход 7 надо ответить ходом 4 (соответственно, на ход 4 нужно ответить ходом 7), а на ход 2 – также ходом 4. В позиции «9» на ход 7 отвечаем ходом 2 (и наоборот), а на ход 4 – тоже ходом 4. Наконец, в позиции «6» возможны только ходы 4 и 2, поэтому все очевидно.

Задача 4: В чашке сидит 105 микробов. За ход разрешается вытащить 2, 3 или 5 микробов. Проигрывает тот, кто не может сделать очередной ход.

Решение: Проигрышными являются позиции вида 7k и 7k + 1. Поскольку 105 – одна из таких позиций, то в игре выигрывает второй игрок.

Задача 5: Конь стоит на поле a1. За ход разрешается передвигать коня на две клетки вправо и одну клетку вверх или вниз, или на две клетки вверх и на одну вправо или влево. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Решение: Проигрывает первый игрок. На доске проигрышными клетками являются только a1, c3, c4, d3, d4, c7, c8, d7, d8, g3, g4, h3, h4, g7, g8, h7, h8.

Задача 6: В кучке n спичек. За ход нужно взять от 1 до 3 спичек, но не столько, сколько только что взял противник. Тот, кто не может сделать ход, проигрывает. Кто выигрывает при правильной игре сторон а) при n = 12 б) при n = 13?

Решение: Для анализа игры нужно понять, что она ведется на поле n × 3, где номер строки соответствует величине последнего хода, сделанного соперником.

Задача 7: В куче – n спичек, из них 3 – обломанные, остальные – целые. За ход можно взять 1, 2 или 3 спички, но обломанные можно брать только когда кончились целые. Тот, кому досталось меньше обломанных спичек, выплачивает разницу в их числе другому. Кто победит и с каким счетом а) при n = 13; б) при n = 14?

Задача 8: Имеется две кучи по семь апельсинов. За ход разрешается съесть один апельсин из любой кучки или по одному апельсину из каждой кучки. Проигрывает тот, кто не сможет сделать ход.

Задача 9: Король стоит на поле a1. За один ход разрешается сдвинуть его на одну клетку вверх, одну клетку вправо или одну клетку по диагонали вправо-вверх. Выигрывает тот, кто поставит короля на поле h8.

Решение: Эти две игры кодируются друг дружкой.

Задача 10:

.7mm

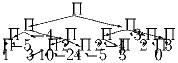
В начале игры фишка стоит на верхней позиции П. Игроки по очереди передвигают ее на одну позицию вниз по линиям. Игра заканчивается, когда фишка попадает на число. После этого второй выплачивает первому столько тугриков, каково это число (если число меньше 0, то на самом деле выплачивает первый второму). Сколько тугриков будет выплачено при наилучшей игре сторон, и какой игрок их получит?

Решение: Второй выплатит первому 2 тугрика.

Задача 11: В трёх кучках лежит по 7 камней. За ход можно взять любое количество камней, но только из одной кучки. Выигрывает взявший последний камень. а) Кто выигрывает в этой игре, если в нее играют 2 человека? б) Докажите, что если в эту игру играют трое, то двое из них могут сговориться и обыграть третьего.

Задача 12: В коробке лежат 300 спичек. За ход можно взять из коробка не более половины имеющихся в нем спичек. Проигрывает тот, кто не может сделать ход.

Решение: Проигрышными позициями («минусами») являются 1, 3, 7, 15, 31, 63, 127 и 255.

Задача 13: На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди откладывают в сторону по одной карточке. Проигрывает тот, после хода которого сумма чисел на отложенных карточках станет больше 25.

Решение: Первый берет карточку с числом 5, а затем дополняет ходы противника до 10.