Задача 1: Можно ли выложить шахматную доску тридцатью двумя доминошками так, чтобы 17 из них были расположены горизонтально, а 15 – вертикально?

Решение: Раскраска «зеброй». Горизонтальные доминошки занимают нечётное число чёрных клеток (а именно – 17), а вертикальные – чётное.

Задача 2: Можно ли выложить квадрат 8 × 8, используя 15 прямоугольников 1 × 4 и один уголок вида ?

Решение: Раскраска «зеброй». Прямоугольники занимают чётное число чёрных клеток, а уголок – нечётное.

Задача 3: Можно ли выложить прямоугольник 6 × 10 прямоугольниками 1 × 4?

Решение: Применим раскраску «в горошек» – покрасим в чёрный цвет те клетки, которые находятся на пересечении чётных вертикалей и чётных горизонталей, а остальные – в белый. Каждый прямоугольник занимает чётное количество чёрных клеток, значит все вместе они тоже занимают чётное число чёрных клеток. Кроме того, проходит шахматная раскраска крупными квадратами 2 × 2 и диагональная четырёхцветная раскраска.

Задача 4: Можно ли сложить квадрат 6 × 6 с помощью 11 прямоугольников 1 × 3 и одного уголка вида ?

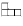Решение: Предположим, что квадрат удалось сложить. Раскрасим клетки в три цвета «по диагоналям», причём так, чтобы, две «крайних» клетки уголка оказались одного цвета (синего). Прямоугольники будут занимать ещё 11 синих клеток, значит все фигурки вместе занимают 13 синих клеток, но синих клеток на доске всего 12.

Другое решение: раскрасим доску «зеброй» в три занумерованных цвета (1, 2, 3) и заметим, что сумма цветов клеток по всей доске делится на 3. С другой стороны, сумма цветов клеток, покрываемых любым прямоугольником 1 × 3, делится на 3, а сумма цветов клеток, покрываемых уголком, не делится на три.

Задача 5: На каждой клетке доски 5 × 5 сидит жук. В некоторый момент времени все жуки взлетают и приземляются на соседние по стороне клетки. Докажите, что при этом окажется хотя бы одна пустая клетка.

Задача 6: Из доски 8 × 8 вырезали угловую клетку. Можно ли оставшуюся часть разрезать на прямоугольники 3 × 1?

Решение: трёхцветная раскраска

Задача 7: Фигура «верблюд» ходит по шахматной доске ходом типа (1, 3). Можно ли пройти ходом «верблюда» с произвольного поля на соседнее?

Решение: Ход верблюда не меняет цвета клетки, на которой он стоит, поэтому на соседнюю клетку перейти он не сможет.

Задача 8: Можно ли доску размером 10 × 10 покрыть фигурами вида ?

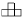Решение: Шахматная раскраска. Каждая такая фигурка занимает нечётное число чёрных клеток, значит все 25 фигурок тоже занимают нечётное число чёрных клеток.

Задача 9: Дана доска 12 × 12. В левом нижнем углу стоят 9 шашек, образуя квадрат 3 × 3. За один ход можно выбрать какие-то две шашки и переставить одну из них симметрично относительно другой (не выходя при этом за пределы доски). Можно ли за несколько ходов переместить эти шашки так, чтоб они образовали квадрат 3 × 3 в правом нижнем углу?

Решение: Нет (шахматная раскраска – шашки остаются на клетках тех же цветов).

Задача 10: В каждой клетке квадрата 9 × 9 сидит жук. По команде каждый жук перелетает на одну из соседних по диагонали клеток. Доказать, что по крайней мере 9 клеток после этого окажутся свободными.

Решение: Раскрасим доску в четыре цвета, так чтобы каждый цвет образовывал раскраску «в горошек». Назовём цвет, в который окрашены угловые клетки, синим, а цвет, в который окрашены клетки, примыкающие к угловым по диагонали – красным. На синие клетки жуки могут перелетать только с красных. Остаётся заметить, что синих клеток на 9 больше, чем красных. Стоит заметить, что мы здесь имеем дело с той же самой шахматной раскраской, но применённой к диагоналям.

Задача 11: Замок имеет форму правильного треугольника, разделенного на 25 маленьких залов той же формы. В каждой стене между залами проделана дверь. Путник ходит по замку, не посещая более одного раза ни один из залов. Найти наибольшее число залов, которое ему удастся посетить.

Решение: 21 зал. Раскрасим треугольник в шахматном порядке. Залов одного цвета (например чёрного) – 15, а другого цвета (белого) – 10. Заметим, что в чёрном зале путник может находиться с самого начала, или попасть в него из белого, поэтому он побывает не более, чем в 11 чёрных залах. Таким образом, не менее 4 чёрных залов останутся непосещёнными. Пример, когда путник не посетит ровно четыре зала, строится без труда.

Задача 12: Дан куб 6 × 6 × 6. Докажите, что его нельзя разбить на параллелепипеды 4 × 1 × 1.

Решение: Трёхмерный вариант задачи 3.

Задача 13: Докажите, что числа от 40 до 99 нельзя разбить на группы по 4 числа так, чтобы числа каждой группы в одном разряде совпадали, а цифры другого разряда шли бы подряд (например «54, 55, 56, 57»; «44, 54, 64, 74»)

Указание: Попытайтесь закодировать эту задачу так, чтобы оправдать её наличие в теме «раскраски».

Решение:

Задача кодируется задачей 3

Задача 14: Докажите, что трёхзначные числа нельзя разбить на группы по 4 так, чтобы числа в каждой группе совпадали во всех разрядах кроме одного, а в оставшемся разряде цифры шли бы подряд.

Решение: Трёхмерный вариант задачи 13 (кодируется задачей очень похожей на задачу 12).