Задача 1:
Найдите все двузначные числа, у которых четвертая степень суммы
цифр равна сумме цифр четвертой степени самого числа.
Решение:
10 и 11.
Задача 2:
Сколько вершин может иметь выпуклый многоугольник, если
известно, что количество его сторон делится на количество его
диагоналей?
Решение:
4 или 5.
Задача 3:
Из единичных кубиков составлен кубик размером 3 × 3 × 3. Какое наибольшее число кубиков можно из него удалить так, чтобы
при взгляде на оставшуюся фигуру с любой из шести возможных сторон был
виден квадрат со стороной 3 без просветов? (Привести пример и
объяснить, почему это наибольшее число.)
Задача 4:
Даны натуральные числа A и B. Известно, что среди четырёх
утверждений «A + 1 делится на B», «A = 2B + 5», «A + B делится на
3», «A + 7B – простое число» имеются три верных и одно неверное.
Найти все возможные пары чисел A и B.
Задача 5:
На витрине лежали N монет, легчайшая из которых весит 100 г, а
каждая следующая – на 1 г тяжелее предыдущей. Какой-то шутник
перепутал все этикетки под монетами, причём продавец все равно помнит,
какая из монет сколько весит, но хозяин ему не верит. В распоряжении
продавца имеются чашечные весы без гирь, которые показывают разность
масс на чашках (в граммах). Как продавцу убедить хозяина в своей
правоте, если а) N = 9 и хозяин согласен провести два взвешивания;
б) N = 27 и хозяин согласен на три взвешивания?
Решение:
а) Первым взвешиванием продавец кладет на одну чашу весов монеты
100, 101, 102, а на другую – монеты 106, 107 и 108. Разность весов
будет равна 18, и эта разность может быть получена только для этого
набора монет, что должно убедить хозяина в том, что взвешены именно
эти монеты. Таким образом, после этого взвешивания имеются три кучки
монет (100,101,102), (103,104,105) и (106,107,108). Вторым
взвешиванием продавец сравнивает 100 + 103 + 106 и 102 + 105 + 108.
Разность весов снова будет максимальной и единственно достижимой.
б) Решается аналогично. Первым взвешиванием на весы кладутся 18
монет.
Задача 6:
Какое наименьшее значение может принимать сумма цифр числа,
кратного 14?
Решение:
2, число 10010
Задача 7:
Кот может съесть гирлянду сосисок за 37 минут, а пес – за 23
минуты. Они начали есть с двух концов, и когда съели всю, то
посчитали, сколько процентов от всей гирлянды досталось каждому.
Оказалось, что коту досталось на 10 больше, чем псу. Кто из них
начал есть раньше и на сколько минут?
Решение:
Кот начал есть гирлянду раньше на 10 минут. Очевидно, что пес
съел 45 или 9/20 всей гирлянды, а кот съел 55 или 11/20 всей
гирлянды. Если кот тратит 37 минут на поедание всей гирлянды, то 55
всей гирлянды он съест за
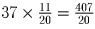
минут. Аналогично, если пес тратит 23 минуты на всю гирлянду, то 45
всей гирлянды он съест за
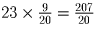
минут. Тогда кот потратил на
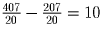
минут больше. Следовательно, кот начал есть гирлянду раньше на 10
минут.
Задача 8:
Найдите а) 18; б) 19; в) 20 наименьших последовательных
натуральных чисел, сумма которых делится на 27.
Решение:
а) числа от 2 до 19; б) числа от 18 до 36; в) от 4 до 23.


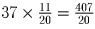 минут. Аналогично, если пес тратит 23 минуты на всю гирлянду, то 45
всей гирлянды он съест за
минут. Аналогично, если пес тратит 23 минуты на всю гирлянду, то 45
всей гирлянды он съест за 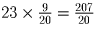 минут. Тогда кот потратил на
минут. Тогда кот потратил на 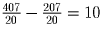 минут больше. Следовательно, кот начал есть гирлянду раньше на 10
минут.
Задача 8:
Найдите а) 18; б) 19; в) 20 наименьших последовательных
натуральных чисел, сумма которых делится на 27.
Решение:
а) числа от 2 до 19; б) числа от 18 до 36; в) от 4 до 23.
минут больше. Следовательно, кот начал есть гирлянду раньше на 10
минут.
Задача 8:
Найдите а) 18; б) 19; в) 20 наименьших последовательных
натуральных чисел, сумма которых делится на 27.
Решение:
а) числа от 2 до 19; б) числа от 18 до 36; в) от 4 до 23.