Задача 1: В Великобритании и США температуру принято измерять по шкале Фаренгейта. Например, температура плавления льда составляет 32\,F, а кипения воды – 212\,F. Существует ли температура, при которой значения в градусах по шкалам Цельсия и Фаренгейта одинаковы?

Решение:  – 40 =  – 40\,F

Задача 2: Начальник отдела, в котором служит Джеймс Бонд, получил приказ об установлении взаимной слежки между агентами с номерами от 001 до 007 по схеме: первый следит за тем, кто следит за вторым, второй – за тем, кто следит за третьим, и так далее, последний следит за тем, кто следит за первым. Но в тот момент, когда начальник составил соответствующую схему, пришло дополнение к приказу – включить в эту группу и агента 008. Какую схему слежки уже составил начальник и сможет ли он составить новую схему?

Решение: Схема имела вид 1-5-2-6-3-7-4-1 (семиугольная звезда). Для восьми агентов решения не существует.

Задача 3: Во фразе, взятой в кавычки, подставьте вместо многоточий числа так, чтобы она оказалась верной.

«В этой фразе используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, причём цифра 0 – … раз, цифра 1 – … раз, цифра 2 – … раз, цифра 3 – … раз, цифра 4 – … раз, цифра 5 – … раз, цифра 6 – … раз, цифра 7 – … раз, цифра 8 – … раз, цифра 9 – … раз».

Решение: 2, 2, 8, 4, 3, 2, 2, 2, 3, 2.

Задача 4: Два человека бегут вниз по ступеням эскалатора метро, идущего вниз. Один бежит быстрее другого. Кто из них насчитает больше ступенек?

Решение: Если они одновременно взойдут на эскалатор, то второй не сосчитает те ступеньки, которые «уйдут» между моментами схода с эскалатора первого и второго человека.

Задача 5: В квадрате 3 × 3 находится 9 лампочек. За одну операцию можно переключить все лампочки, находящиеся в каком-нибудь квадрате 2 × 2. Сколько различных узоров можно получить из «погасшего» состояния?

Решение: Так как все определяется угловыми лампочками, то узоров 2⁴ = 16.

Задача 6: Можно ли в вершинах и на серединах сторон правильного восьмиугольника расставить натуральные числа от 1 до 16 так, чтобы сумма чисел на концах любой стороны равнялась числу в его середине? Каждое из чисел можно использовать ровно 1 раз.

Решение: Нельзя, так как тогда сумма всех чисел от 1 до 16 должна быть кратна 3.

Задача 7: У Кащея есть куб, в каждой вершине которого вставлено по алмазу. Известны веса этих алмазов: 1 карат, 2 карата, …, 8 карат. Кащей предлагает Ивану-Царевичу следующую игру: он называет сумму весов алмазов на каждом ребре. Если после этого Иван сможет правильно определить, в какой вершине какой алмаз, то он получает драгоценный куб, а если нет, то распрощается с жизнью. Стоит ли Ивану соглашаться на такую игру?

Задача 8: Найдите наименьшее натуральное число, которое после деления на 2 становится квадратом, а после деления на 3 – кубом целого числа.

Решение: 648.

Задача 9: Есть четыре утверждения: «2x + y + z – простое число», «x + 2y + z – простое число», «x + y + 2z – простое число», «x,y,z – натуральные числа». Докажите, что все четыре утверждения не могут быть верными одновременно.

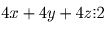
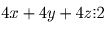Решение: Сложив все три суммы, получим . Но все три суммы – простые числа большие двух, а значит нечётны.