Задача 1:
Найти наименьшее натуральное число, записанное с помощью двоек и
троек, у которого сумма и произведение цифр делятся на 6.
Задача 2:
В Котельниче собрались школьники, едущие в Вишкиль. На первом
автобусе уехал каждый десятый школьник, на втором – каждый седьмой из
оставшихся, а затем на третьем – каждый пятый из оставшихся на данный
момент. В итоге 111 школьников осталось ждать других автобусов.
Сколько школьников изначально стояло на остановке в Котельниче?
Задача 3:
Можно ли на плоскости отметить 6 точек и соединить их
непересекающимися отрезками (с концами в этих точках) так, чтобы из
каждой точки выходило ровно по 4 отрезка?
Задача 4:
В столовую привезли халву, но в дороге она раскрошилась на 2000
частей. Константин Александрович сказал, что он сможет разложить халву
на две кучки равной массы, сделав не более N разрезов. Какое
наименьшее N мог назвать Константин Александрович, если разломанную
халву он еще не видел?
Задача 5:
Барон Мюнхгаузен говорит, что, как бы ни стояли на шахматной
доске 6 ладей, не бьющих друг друга, он всегда сможет добавить еще
коня так, чтобы ни одна из фигур не била другую. Прав ли он?
Задача 6:
Решите ребус
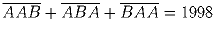
, если одинаковым
цифрам соответствуют одинаковые буквы, а разным – разные.
Задача 7:
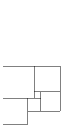
Фигура на рисунке составлена из квадратов. Найдите сторону
левого нижнего квадрата, если сторона самого маленького квадрата
равна 1.
Задача 8:
Федоту выставили годовые оценки по 12 предметам. Оказалось, что
его средний балл равен 3,5. По скольким предметам в следующем году
он должен улучшить свою оценку на один балл для того, чтобы средний
балл стал равен 4?


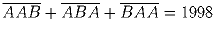 , если одинаковым
цифрам соответствуют одинаковые буквы, а разным – разные.
Задача 7:
Фигура на рисунке составлена из квадратов. Найдите сторону
левого нижнего квадрата, если сторона самого маленького квадрата
равна 1.
, если одинаковым
цифрам соответствуют одинаковые буквы, а разным – разные.
Задача 7:
Фигура на рисунке составлена из квадратов. Найдите сторону
левого нижнего квадрата, если сторона самого маленького квадрата
равна 1.