Задача 1:
Какое наибольшее число слонов можно добавить к шести ладьям так,
чтобы ни одна из шахматных фигур на доске не била другую?
Решение:
4
Задача 2:
В классе 21 человек. Никакие две девочки не дружат с одинаковым
количеством мальчиков. Какое наибольшее количество девочек может быть
в классе?
Решение:
Построим пример для 11 девочек. Первая девочка дружит с нулем
мальчиков, вторая девочка дружит с одним мальчиком, третья – с двумя
мальчиками и так далее. Тогда одиннадцатая девочка дружит с 10
мальчиками. Докажем, что больше 11 девочек быть не может. Если в
классе больше 11 девочек, то там меньше 10 мальчиков. Тогда различных
вариантов количества мальчиков, с которыми можно дружить, всего 0, 1,
2, n, где n - количество мальчиков в классе , n < 10. Тогда
вариантов n + 1 < 11. А девочек больше 11. Противоречие.
Задача 3:
Может ли шахматный конь (который ходит по правилам) обойти все
поля доски 4 × 4, побывав на каждом поле ровно один раз, и
вернуться на ту же клетку? Начинать разрешается на любом поле.
Решение:
Так как нам надо вернуться на ту же клетку, то путь коня можно
считать замкнутым. Назовем поля b2 и c3, узловыми для угловых
полей a4 и d1. Заметим, что с любого из этих двух полей, и только
с них, можно попасть на угловые поля a4 и d1. Так как путь
замкнут, то на каждое поле необходимо попасть с какого-нибудь поля, а
затем выйти на другое. Пусть первым на пути коня встречается поле
a4. На него конь может попасть только с одного из узловых полей.
Тогда выйти с этого поля он может только на другое узловое поле. Но в
этом случае на следующем ходе он обязан встать на поле d4, так как
если он на него не встанет, то больше он на узловые поля не попадет
(на каждом поле он бывает только один раз), а только с узловых полей
он может попасть на поле d4. Таким образом, он обязан встать на поле
d4, но далее с этого поля он выйти уже не сможет, так как на обоих
узловых полях он уже побывал, и на них он больше встать не может.
Отсюда получаем, что требуемого маршрута не существует.
Задача 4:
Разрежьте правильный шестиугольник на 8 равных частей.
Задача 5:
Три девочки и три мальчика в течение года решали одни и те же
задачи. Катя решила ¾ всех задач и еще ¼ от того, что
решил Петя. Лена решила ½ всех задач и еще
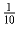
того,
что решил Вася. Маша решила
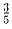
всех задач и еще
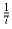
от
того, что решил Федя. Какая из девочек решила больше всех задач?
Решение:
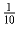
того, что решил Вася – это не больше, чем
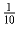
общего числа задач. Поэтому Лена решила не больше, чем
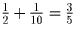
всех задач. Аналогично, Маша решила не
больше, чем
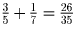
всех задач. С другой
стороны, Катя решила не меньше ¾ всех задач. Поскольку
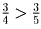
и
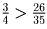
, среди девочек больше всех
задач решила Катя.
Задача 6:
Три команды играли в КВН. Перед игрой игрок Иванов перешел из
первой команды во вторую, игрок Сидоров перешел из второй команды в
третью, а игрок Петров перешел из третьей команды в первую. После
этого средний возраст первой команды увеличился на 1 неделю, второй –
увеличился на 2 недели, а третьей – уменьшился на 4 недели. Известно,
что в первой и во второй команде по 12 игроков. Сколько игроков в
третьей команде?
Решение:
Общий возраст первой команды увеличился на 12 недель, а
второй – на 24 недели. Так как общий возраст всех команд при этом не
изменился, то общий возраст третьей команды уменьшился на 36 недель,
поэтому в ней 9 игроков.
Задача 7:
В квадрате 3 × 3 расставлены числа так, чтобы суммы чисел в
каждой строке, каждом столбце и на каждой большой диагонали равны
нулю. Известно, что сумма квадратов чисел в верхней строке равна 2000.
Чему может быть равна сумма квадратов чисел в нижней строке?
Решение:
Сложим все числа в таблице. Сумма равна нулю. Вычтем теперь
большие диагонали, средний столбец и среднюю строку. Все числа, кроме
среднего, мы вычли 1 раз, а среднее – 4 раза. Все это дело опять
равно нулю, следовательно, в середине стоит ноль. Тогда на концах
одной и той же большой диагонали, а так же на концах среднего столбца
стоят противоположные числа. Следовательно, в третьей строке стоят
числа, противоположные числам первой строки, а сумма квадратов та же.


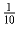 того,
что решил Вася. Маша решила
того,
что решил Вася. Маша решила 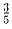 всех задач и еще
всех задач и еще 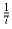 от
того, что решил Федя. Какая из девочек решила больше всех задач?
Решение:
от
того, что решил Федя. Какая из девочек решила больше всех задач?
Решение:
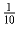 того, что решил Вася – это не больше, чем
того, что решил Вася – это не больше, чем
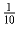 общего числа задач. Поэтому Лена решила не больше, чем
общего числа задач. Поэтому Лена решила не больше, чем
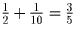 всех задач. Аналогично, Маша решила не
больше, чем
всех задач. Аналогично, Маша решила не
больше, чем 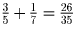 всех задач. С другой
стороны, Катя решила не меньше ¾ всех задач. Поскольку
всех задач. С другой
стороны, Катя решила не меньше ¾ всех задач. Поскольку
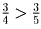 и
и 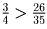 , среди девочек больше всех
задач решила Катя.
Задача 6:
Три команды играли в КВН. Перед игрой игрок Иванов перешел из
первой команды во вторую, игрок Сидоров перешел из второй команды в
третью, а игрок Петров перешел из третьей команды в первую. После
этого средний возраст первой команды увеличился на 1 неделю, второй –
увеличился на 2 недели, а третьей – уменьшился на 4 недели. Известно,
что в первой и во второй команде по 12 игроков. Сколько игроков в
третьей команде?
Решение:
Общий возраст первой команды увеличился на 12 недель, а
второй – на 24 недели. Так как общий возраст всех команд при этом не
изменился, то общий возраст третьей команды уменьшился на 36 недель,
поэтому в ней 9 игроков.
Задача 7:
В квадрате 3 × 3 расставлены числа так, чтобы суммы чисел в
каждой строке, каждом столбце и на каждой большой диагонали равны
нулю. Известно, что сумма квадратов чисел в верхней строке равна 2000.
Чему может быть равна сумма квадратов чисел в нижней строке?
Решение:
Сложим все числа в таблице. Сумма равна нулю. Вычтем теперь
большие диагонали, средний столбец и среднюю строку. Все числа, кроме
среднего, мы вычли 1 раз, а среднее – 4 раза. Все это дело опять
равно нулю, следовательно, в середине стоит ноль. Тогда на концах
одной и той же большой диагонали, а так же на концах среднего столбца
стоят противоположные числа. Следовательно, в третьей строке стоят
числа, противоположные числам первой строки, а сумма квадратов та же.
, среди девочек больше всех
задач решила Катя.
Задача 6:
Три команды играли в КВН. Перед игрой игрок Иванов перешел из
первой команды во вторую, игрок Сидоров перешел из второй команды в
третью, а игрок Петров перешел из третьей команды в первую. После
этого средний возраст первой команды увеличился на 1 неделю, второй –
увеличился на 2 недели, а третьей – уменьшился на 4 недели. Известно,
что в первой и во второй команде по 12 игроков. Сколько игроков в
третьей команде?
Решение:
Общий возраст первой команды увеличился на 12 недель, а
второй – на 24 недели. Так как общий возраст всех команд при этом не
изменился, то общий возраст третьей команды уменьшился на 36 недель,
поэтому в ней 9 игроков.
Задача 7:
В квадрате 3 × 3 расставлены числа так, чтобы суммы чисел в
каждой строке, каждом столбце и на каждой большой диагонали равны
нулю. Известно, что сумма квадратов чисел в верхней строке равна 2000.
Чему может быть равна сумма квадратов чисел в нижней строке?
Решение:
Сложим все числа в таблице. Сумма равна нулю. Вычтем теперь
большие диагонали, средний столбец и среднюю строку. Все числа, кроме
среднего, мы вычли 1 раз, а среднее – 4 раза. Все это дело опять
равно нулю, следовательно, в середине стоит ноль. Тогда на концах
одной и той же большой диагонали, а так же на концах среднего столбца
стоят противоположные числа. Следовательно, в третьей строке стоят
числа, противоположные числам первой строки, а сумма квадратов та же.