 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Разрезания и перекладывания | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2000 г, 6 класс. Разрезания и перекладывания |
|
|
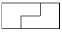
Задача 2: Дан круг и отмечена точка внутри него. На какое минимальное количество частей можно разрезать этот круг так, чтобы из получившихся частей можно было сложить круг, в котором отмеченная точка является центром. Решение: Вырежем круг с диаметром AO (вернее чуть больше) и повернём его на 180. Задача 3: Разрежьте уголок, составленный из трёх клеток (
 ),
на четыре равные по форме части.
Задача 4:
С помощью разрезаний и перекладываний сделайте из фигуры «крест»
фигуру «конфета» (см. рисунок).
),
на четыре равные по форме части.
Задача 4:
С помощью разрезаний и перекладываний сделайте из фигуры «крест»
фигуру «конфета» (см. рисунок).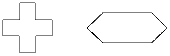
Решение:
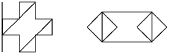
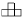 на пять частей и сложите из них два равных
квадрата.
Решение:
на пять частей и сложите из них два равных
квадрата.
Решение: 
a) с помощью разрезаний и перекладываний;
b) с помощью только разрезаний.
Решение: Задача 7:
a) Можно ли разрезать квадрат на 100 равных четырёхугольников,
не являющихся прямоугольниками? б) Можно ли разрезать квадрат на 2000 равных
треугольников?
Задача 8:
Можно ли сложить квадрат из фигурок
Задача 7:
a) Можно ли разрезать квадрат на 100 равных четырёхугольников,
не являющихся прямоугольниками? б) Можно ли разрезать квадрат на 2000 равных
треугольников?
Задача 8:
Можно ли сложить квадрат из фигурок 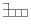 ? Фигурки можно брать в
неограниченном количестве. А если длинная сторона уголка равна n клеткам?
Задача 9:
Можно ли замостить плоскость одинаковыми a) пятиугольниками;
б) шестиугольниками; в) семиугольниками?
Задача 10:
Разрежьте квадрат на два одинаковых а) пятиугольника; б) шестиугольника;
в) 2n-угольника; г) 2n + 1-угольника. Можно ли разрезать так прямоугольник?
Для каких еще фигур годится этот алгоритм?
Задача 11:
Можно ли разрезать на четыре остроугольных треугольника a) какой-нибудь
пятиугольник; б) правильный пятиугольник?
? Фигурки можно брать в
неограниченном количестве. А если длинная сторона уголка равна n клеткам?
Задача 9:
Можно ли замостить плоскость одинаковыми a) пятиугольниками;
б) шестиугольниками; в) семиугольниками?
Задача 10:
Разрежьте квадрат на два одинаковых а) пятиугольника; б) шестиугольника;
в) 2n-угольника; г) 2n + 1-угольника. Можно ли разрезать так прямоугольник?
Для каких еще фигур годится этот алгоритм?
Задача 11:
Можно ли разрезать на четыре остроугольных треугольника a) какой-нибудь
пятиугольник; б) правильный пятиугольник?Задача 12:
На картинках приведены фигуры на клетчатой бумаге. Ваша задача – разрезать каждую фигуру на две одинаковых (по форме и размерам) части.
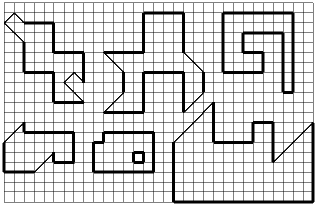
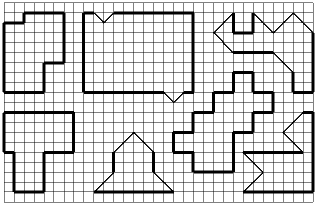
(Фигурку, похожую на ракету надо разбить на четыре одинаковые части)
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 6 класс >> Разрезания и перекладывания | Убрать решения |