 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Бином Ньютона и биномиальные коэффициенты (профи) | Убрать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Бином Ньютона и биномиальные коэффициенты (профи) |
|
|
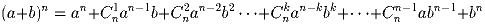
Задача 4: Выпишите формулы для а) (a + b)4 ; б) (x + 1)n; в) (a – b)n. Задача 5: Докажите следующие свойства биномиальных коэффициентов двумя способами – алгебраически и комбинаторно:
а) 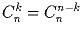 ;
;
б) 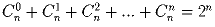 ;
;
в) 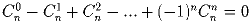 ;
;
г) 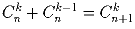 .
.
а) если 1 ≤ k ≤ p – 1, то 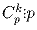 ;
;
б) (a + b)p ≡ pap + bp;
в) 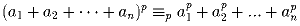 ;
;
г) (малая теорема Ферма) 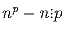 при любом целом n.
при любом целом n.
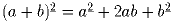 ; б)
; б)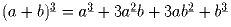 .
Задача 9:
.
Задача 9:
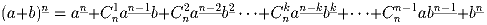
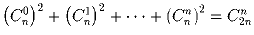 .
.Зад12. Докажите, что 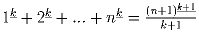 при целых n,k ≥ 0
при целых n,k ≥ 0
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Бином Ньютона и биномиальные коэффициенты (профи) | Убрать решения |