 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Решение линейных уравнений в целых числах | Убрать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Решение линейных уравнений в целых числах |
|
|
а) x – y = 0;
б) 5x – 3y = 0;
в) 15x + 9y = 0.
Задача 2: Решите в целых числах уравнение 15x – 9y = – 7. Задача 3: На прямой сидит блоха, которая может прыгать на 5 см или 7 см вправо или влево. Сможет ли она сместиться после нескольких прыжков вправо на 3 см от начального положения? Если сможет, то как она должна прыгать? Задача 4: Решите в целых числах уравнение 5x – 7y = 3:а) найдите какое-нибудь одно решение;
б) найдите какие-нибудь три решения;
в) если выполнены равенства 5x1 – 7y1 = 3 и 5y2 – 7y2 = 3, то рассмотрите их разность;
г) найдите все решения уравнения 5x – 7y = 3 в целых числах.
Задача 5: Решите в целых числах уравнения:а) 3x + 5y = 13;
б) 10x + 15y = – 5;
в) – 6x + 21y = 18.
Задача 6: Решите в натуральных числах уравнение 2000x + 513y = 2513. Задача 7: Решите в целых числах уравнение 2000x + 513y = 329. Задача 8: Пусть a и b – натуральные числа и a > b. Поделим a на b с остатком: a = bq + r, 0 ≤ r < b.а) Докажите, что НОД (a,b) = НОД (a – b,b).
б) Докажите, что НОД (a,b) = НОД (r,b).
в) Сформулируйте правило для поиска НОД двух «больших» чисел.
Задача 9: Найдите: а) НОД (2000,502); б) НОД (589,1426). Задача 10: Могут ли числа 2n + 13 и n + 7 при натуральном n иметь общий множитель, больший чем 1? Задача 11: Докажите, что для каждого натурального n дробь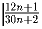
несократима.
Задача 12:
а) Докажите, что если НОД (a,b) = 1,
то уравнение ax + by = 1 имеет решение в
целых числах.б) Докажите, что если НОД (a,b) = d, то уравнение ax + by = d имеет решение в целых числах.
в) Докажите, что если НОД (a,b) = d и c делится на d, то уравнение ax + by = c имеет решение в целых числах.
г) Докажите, что если НОД (a,b) = d и c не делится на d, то уравнение ax + by = c не имеет решений в целых числах.
Задача 13: Решите в целых числах уравнение 2000x + 513y = 329. Задача 14: Решите в целых числах уравнения:
а) – 7x + 4y + 9z = 89;
б) 10x + 13y + 8z = 143.
Задача 15: На бесконечной шахматной доске стоит конь. Докажите, что он сможет прискакать в любую клетку. Задача 16: На прямой сидит блоха, которая может прыгать на 5 см влево или на 7 см вправо. В каких точках прямой может побывать эта блоха?| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Решение линейных уравнений в целых числах | Убрать решения |