 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Игры-2 | Убрать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Игры-2 |
|
|
Задача 2: Ферзь стоит на поле с1. За ход его разрешается передвинуть на любое число полей вправо, вверх или по диагонали «вправо-вверх». Выигрывает тот, кто поставит ферзя на поле h8. Задача 3: В одной куче 18 конфет, в другой – 23. Двое по очереди съедают одну из куч, а другую делят на две кучи. Тот, кто не может поделить кучу (в ней одна конфета) , проигрывает. Задача 4: На столе лежат 20 спичек. Игрок может взять 2, 3, или 4 спички, но не может взять столько, сколько взял предыдущий. Кто не может сходить – проигрывает.
Задача 5:
В каждой вершине дерева написано число. В корневой вершине графа лежит фишка. Игроки по очереди передвигают ее вдоль ребер, причем запрещается возвращать фишку в вершину, где она уже побывала. Игра заканчивается, если какой-нибудь игрок не может сделать очередной ход. В этом случае он получает от второго игрока сумму, написанную на последней вершине (если она отрицательна, то он платит сам) . Выигрывает тот, кто получит деньги от другого игрока. Кто выигрывает при правильной стратегии и какой наибольший выигрыш он может себе гарантировать независимо от ходов противника?
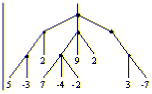
Задача 6:
Два игрока по очереди ходят ладьей, начиная с верхнего поля. При этом запрещается ставить ладью на поле, где она уже побывала. Проигрывает игрок, который не может сделать ход.

Задача 7:
На горизонтальной полоске 4 × 1 слева стоят две фишки. За ход нужно передвинуть одну из фишек на любое свободное поле (перепрыгивать через фишки нельзя). Проигрывает игрок, после хода которого возникает позиция, уже встречавшаяся ранее.
Задача 8:Леонид Михайлович и Ольга Викторовна играют на бесконечной полоске клетчатой бумаги в следующую игру. Леонид Михайлович ставит два крестика, а Ольга Викторовна стирает любое число подряд идущих крестиков. Сможет ли Ольга Викторовна помешать Леониду Михайловичу выставить 2000 крестиков в ряд?
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Игры-2 | Убрать решения |