Задача 1:
Найдите наибольший общий делитель всех девятизначных чисел, состоящих из
цифр 1,2,3,4,5,6,7,8,9 (без повторений).
Задача 2:
Какое наибольшее количество месяцев одного года могут иметь по пять пятниц?
Задача 3:
Треугольник разрезали на два многоугольника прямолинейным разрезом, один из
полученных многоугольников вновь разрезали на два и т. д. Какое наименьшее
количество разрезов следует произвести, чтобы общее количество вершин у
полученных многоугольников стало равным 2000?
Задача 4:
В трех ящиках лежат орехи. В первом на 99 орехов меньше, чем в двух других
вместе, во втором – на 19 меньше, чем в первом и третьем вместе. Сколько
орехов лежит в третьем ящике?
Задача 5:
Из пункта А в пункт Б и из пункта Б в пункт А одновременно выбежали два
спортсмена. Когда первоначальное расстояние между ними сократилось на 15 км,
то первому из спортсменов осталось бежать до пункта Б в три раза большее
расстояние, чем было между ними в это время, а второму – в полтора раза
больше, чем он пробежал. Каково расстояние между пунктами?
Задача 6:
Все натуральные числа от 1 по 1000 разбиты на две группы: четные и нечетные
числа. Определите, для какой из групп сумма всех цифр, используемых для
записи чисел, больше, и на сколько?
Задача 7:
В прямоугольном треугольнике наименьшая высота вчетверо короче гипотенузы.
Чему равны углы треугольника?
Задача 8:
При умножении пятизначного натурального числа на девять получилось число,
записанное теми же цифрами, но в обратном порядке. Найдите все такие числа.
Задача 9:
В ящике лежат 1999 белых шаров, 2000 красных шаров и 2001 синий шар. Какое
наименьшее число шаров нужно взять из ящика, не заглядывая внутрь, чтобы
среди взятых шаров наверняка были шары всех цветов?
Задача 10:
Найдите все натуральные числа, которые при удвоении записываются теми же
цифрами, что и квадраты этих чисел, только в обратном порядке.
Задача 11:
Четверо бизнесменов участвовали в соревновании на звание самого лучшего.
Первый, четвертый и третий бизнесмены вместе заработали в четыре раза больше
второго, второй, третий и четвертый бизнесмены вместе заработали в три раза
больше первого. И, наконец, первый, второй и третий бизнесмены вместе
заработали в два раза больше четвертого. Кто на каком месте оказался в этом
соревновании?
Задача 12:
Квадраты натуральных чисел выписаны в ряд: 149162536... Какая цифра стоит на
1998 месте?
Задача 13:
Какое наибольшее число элементов содержит множество А, если оно имеет больше
19-элементных подмножеств, чем 98 элементных?
Задача 14:
Поезд проехал переезд автотрассы шириной 5 метров за 5 секунд, а мимо
перрона длиной 200 метров за 15 секунд, двигаясь вдвое медленнее. Какова
длина состава?
Задача 15:
15 одинаковых шариков можно сложить в виде треугольника, но нельзя сложить в
виде квадрата – одного шарика не хватает. Из какого количества шариков, не
превосходящего 50, можно сложить как треугольник, так и квадрат?
Задача 16:
Найдите наименьшее натуральное число, которое оканчивается на 13, делится на
13 и имеет сумму цифр, равную 13.
Задача 17:
Сколько имеется прямоугольных треугольников, длины сторон которых выражаются
целыми числами, если один из катетов этих треугольников равен 15?
Задача 18:
Найдите правильную дробь, которая увеличивается в 3 раза, если ее числитель
возвести в куб, а к знаменателю прибавить 3.
Задача 19:
Найдите восемь последовательных целых чисел, сумма первых трех из которых
равна сумме остальных пяти.
Задача 20:
Сколько последовательных натуральных чисел, начиная с 1, надо сложить, чтобы
получить трехзначное число, записываемое одинаковыми цифрами?
Задача 21:
Первая цифра четырехзначного числа равна количеству нулей в этом числе,
вторая цифра равна числу единиц, третья – числу двоек, четвертая – числу
троек. Найдите все такие числа.
Задача 22:
Трехзначное число начинается с цифры 7. Из него получили другое трехзначное
число, переставив эту цифру в конец числа. Полученное число оказалось на 117
меньше предыдущего. Какое число рассматривалось?
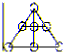
Задача 23: В кружках треугольника расставлены все цифры от 1 по 7
(каждое по одному разу), причем сумма чисел вдоль каждого
отрезка прямой одна и та же. Чему она равняется и какие
числа поставлены в вершины треугольника? (Приведите хотя бы один
из вариантов расстановки)
Задача 24:
Найдите какое-нибудь решение числового ребуса:
* * *
* * *
------
* * * *
* * *
---------
a a a a a


