Задача 1: Найдите закономерность и продолжите ряд 2, 5, 8, 11, .

Задача 2: Найдите 2000-ый член последовательности из задания 1. Найдите ее n-ый член.

Задача 3: Напишите формулу общего члена арифметической прогрессии:

а) с первым членом a и вторым членом a + d;

б) с первым членом a и вторым членом b.

Задача 4: В следующих последовательностях найдите члены a₂₅ и a₄₀:

а) 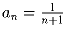; б) a_n = n² – 5n; в) .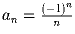

Задача 5: Найдите сумму первых 2000 членов арифметической прогрессии из задания №1. Чему равна сумма первых n ее членов? Чему равна сумма всех членов этой прогрессии с номерами с сотого по двухсотый?

Задача 6: Найдите сумму первых 15 членов арифметической прогрессии, если ее восьмой член равен 11.

Задача 7: Найдите сумму всех четырехзначных чисел, делящихся на 30.

Задача 8: Найдите сумму всех трехзначных чисел, не делящихся ни на 2, ни на 3.

Задача 9: Сумма номеров домов на одной стороне квартала 247. Найдите номер дома, седьмого от угла.

Задача 10: Найдите закономерность и продолжите ряд 2, 6, 18, 54, . Какое число окажется на десятом месте? На 2000-м месте? На n-ом месте?

Задача 11: Напишите формулу общего члена геометрической прогрессии:

а) с первым членом a и вторым членом aq.

б) с первым членом a и вторым членом b.

Задача 12: Первый член геометрической прогрессии – целое число, а каждый следующий ее член больше предыдущего в целое число раз. Найдите пятый член этой прогрессии, если произведение первых четырех ее членов равно: а) 5184; б)  3456.

Задача 13: а) Докажите, что последовательность (a_n) является арифметической прогрессией в том и только в том случае, если при всех n ≥ 2 справедливо равенство 2a_n = a_n – 1 + a_n + 1.

б) Сформулируйте и докажите аналогичное свойство геометрической прогрессии.

Задача 14: Найдите общий член ряда: а) 13, 19, 25,; б) 12, 18, 27,; в) 1, 4, 9,; г) 1/2, 1/6, 1/12, 1/20,

Задача 15: Найдите сумму первых 100 членов геометрической прогрессии 3, 12, 48,

Задача 16: Цифры каждого из трех трехзначных чисел составляют арифметическую прогрессию, сумма этих чисел 750. Найдите трехзначные числа.

Задача 17: Все члены арифметической прогрессии – натуральные числа. Докажите, что среди них найдется такое число, в записи которого имеется хоть один нуль. Найдите сумму 1+11+111+ + 1111.