Задача 1:
У составного числа a найдется такой простой делитель p, что
p² ≤ a.
Задача 2:
Как проверить, что числа 1997 и 1999 – простые?
Задача 3:
Найдите НОД (99! + 100!,101!).
Задача 4:
Докажите, что простых чисел бесконечно много.
Задача 5:
а) Найдутся ли 3 натуральных числа таких, что ни одно из них
не делится на другое, а произведение любых двух из них делится на третье? б)
Тот же вопрос про 10 чисел?
Задача 6:
Докажите, что

.
Задача 7:
Каким может при натуральных n быть НОД чисел а) 2n – 17 и n – 8; б)
13n + 8 и 8n + 5?
Задача 8:
Докажите, что если a = bq + r, то НОД (a,b) = НОД (b,r).
Задача 9:
Найдите а) НОД (1998,8991); б) НОД (7387,82861).
Задача 10:
Найдите а)
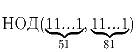
; б) НОД (2¹ºº – 1,2¹²º – 1);
в) НОД (2
m – 1,2
n – 1).
Задача 11:
На прямой сидит блоха, и прыгает всякий раз либо на 15
сантиметров вправо, либо на 21 сантиметр влево. В каких точках прямой может
побывать эта блоха?
Задача 12:
В банке 500 долларов. Разрешаются две операции: взять из
банка 300 долларов или положить в него 198 долларов. Эти операции можно
проводить много раз, при этом, однако, никаких денег, кроме тех, что
первоначально лежат в банке, нет. Какую максимальную сумму можно извлечь из
банка и как это сделать?
Задача 13:
Докажите, что
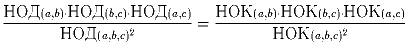 Задача 14:
Задача 14:
При каких n можно найти n натуральных чисел,
сумма которых равна их НОК?
Задача 15:
Докажите, что в вершинах любого многогранника можно
расставить натуральные числа так, чтобы числа в вершинах связанных ребром
имели общий делитель больше 1, а не связанные ребром не имели.
Задача 16:
Докажите основную теорему арифметики (ОТА):
- Если r – остаток от деления a на b, то НОД (a,b) = НОД (b,r).
- Если d = НОД (a,b), то найдутся такие целые m и n, что
d = ma + nb.
- Если a не делится на простое число p, то найдутся целые m и n,
что 1 = ma + np.
- Если
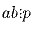 , где p – простое, то
, где p – простое, то 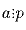 либо
либо 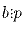 .
. - (ОТА) Разложение натурального числа в произведение простых
сомножителей единственно с точностью до порядка сомножителей.
Задача 17:
Числа a, b, c – целые.
Докажите, что уравнение ax + by = c имеет
решение в целых числах тогда и только тогда, когда
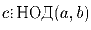
.


 .
Задача 7:
Каким может при натуральных n быть НОД чисел а) 2n – 17 и n – 8; б)
13n + 8 и 8n + 5?
.
Задача 7:
Каким может при натуральных n быть НОД чисел а) 2n – 17 и n – 8; б)
13n + 8 и 8n + 5?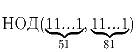 ; б) НОД (2¹ºº – 1,2¹²º – 1);
в) НОД (2m – 1,2n – 1).
Задача 11:
На прямой сидит блоха, и прыгает всякий раз либо на 15
сантиметров вправо, либо на 21 сантиметр влево. В каких точках прямой может
побывать эта блоха?
Задача 12:
В банке 500 долларов. Разрешаются две операции: взять из
банка 300 долларов или положить в него 198 долларов. Эти операции можно
проводить много раз, при этом, однако, никаких денег, кроме тех, что
первоначально лежат в банке, нет. Какую максимальную сумму можно извлечь из
банка и как это сделать?
Задача 13:
Докажите, что
; б) НОД (2¹ºº – 1,2¹²º – 1);
в) НОД (2m – 1,2n – 1).
Задача 11:
На прямой сидит блоха, и прыгает всякий раз либо на 15
сантиметров вправо, либо на 21 сантиметр влево. В каких точках прямой может
побывать эта блоха?
Задача 12:
В банке 500 долларов. Разрешаются две операции: взять из
банка 300 долларов или положить в него 198 долларов. Эти операции можно
проводить много раз, при этом, однако, никаких денег, кроме тех, что
первоначально лежат в банке, нет. Какую максимальную сумму можно извлечь из
банка и как это сделать?
Задача 13:
Докажите, что
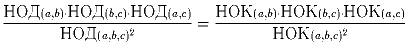 Задача 14:
При каких n можно найти n натуральных чисел,
сумма которых равна их НОК?
Задача 15:
Докажите, что в вершинах любого многогранника можно
расставить натуральные числа так, чтобы числа в вершинах связанных ребром
имели общий делитель больше 1, а не связанные ребром не имели.
Задача 16:
Докажите основную теорему арифметики (ОТА):
Задача 14:
При каких n можно найти n натуральных чисел,
сумма которых равна их НОК?
Задача 15:
Докажите, что в вершинах любого многогранника можно
расставить натуральные числа так, чтобы числа в вершинах связанных ребром
имели общий делитель больше 1, а не связанные ребром не имели.
Задача 16:
Докажите основную теорему арифметики (ОТА):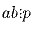 , где p – простое, то
, где p – простое, то 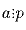 либо
либо 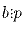 .
.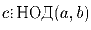 .
.