Задача 1:
Расставьте несколько фигур на шахматной доске так, чтобы рядом с каждой
фигурой было ровно три свободных поля, а рядом с каждым свободным полем –
ровно одна фигура? (Примечание: рядом – значит в клетке с общей стороной).
Задача 2: На острове Рыцарей и Лжецов стоит замок. В замке 2000 комнат. В третьей по
величине комнате (после тронного зала и подвала) стоит круглый стол. За этим
столом сидят 16 аборигенов. разного возраста и звания. На вопрос: «Не считая
вас и двух ваших соседей, кто все остальные?», каждый сидящий ответил: «Все
они лжецы». Сколько лжецов сидит за столом?
Задача 3:
На доске написано число. Разрешается умножить или поделить его на любое
простое число. Можно ли ровно за 2000 таких операций из 1 получить 2000?
Задача 4:
a, b и c - целые числа. Докажите, что если
a = b + c, то a
4 + b
4 + c
4 есть удвоенный квадрат целого числа.
Задача 5:
В выпуклом четырёхугольнике соединены середины двух противоположных сторон.
Оказалось, что одна диагональ делит этот отрезок пополам. Докажите, что эта
диагональ делит площадь четырехугольника тоже пополам.
Задача 6:
2000 яблок лежат в нескольких корзинах. Разрешается убирать корзины и
вынимать яблоки из корзин. Докажите, что можно добиться того, чтобы во всех
оставшихся корзинах было поровну яблок, а общее число яблок было не меньше 100.
Задача 7:
На сторонах треугольника ABC вне его построены правильные
треугольники ABD и
BCE. Отрезки CD и AE пересекаются в точке M. Докажите, что
AM + BM + CM = CD.
Задача 8:
Проказница мартышка, осел, козел да косолапый мишка подружились с козой (с
баяном) и затеяли сыграть квинтет. Пришли на лужок, сели в кружок, но музыка
не пошла. Тогда друзья стали пересаживаться. За одну пересадку меняется
местами одна пара соседей. Друзья не успокоятся, пока каждый не посидит на
каждом месте. Каким наименьшим количеством пересадок они могут обойтись?
Задача 9:
Плоскость разграфлена на квадратные ячейки единичной площади. Докажите, что
любой многоугольник площади меньше 1 можно расположить на этой плоскости
так, чтобы внутрь него не попало ни одного узла решетки.
Задача 10:
Луч разбит на отрезки длины 1. Блоха из начала луча прыжками длины
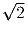
ускакала в бесконечность. Покрасим отрезки, где она побывала, а также
самый первый. Докажите, что кузнечик может из начала луча ускакать в
бесконечность прыжками некоторой постоянной длины C так, чтобы побывать в
точности на всех неокрашенных отрезках.
Задача 11:
Докажите, что площадь треугольника с вершинами в узлах сетки не менее
½.
Задача 12:
Стороны прямоугольника на шахматной доске параллельны сторонам доски.
Докажите, что разность суммарных площадей белых и черных частей
прямоугольника не превосходит площади одной клетки.
Задача 13:
Докажите неравенство для площади четырехугольника (a,b,c,d –
стороны по
порядку):
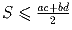
.
Задача 14:
(Принцип Кавальери)
а) На плоскости нарисованы два выпуклых многоугольника и прямая. Известно,
что любая прямая, параллельная данной, пересекается с многоугольниками по
отрезкам раной длины. Докажите, что эти многоугольники равновелики. б)
Докажите, что два равновеликих прямоугольника можно расположить на плоскости
так, что они будут пересекаться по равным отрезкам с любой прямой,
параллельной данной.
Задача 15:
(Корректность площади: решать, не используя понятия площади)
а) Прямоугольник разрезали на несколько меньших
прямоугольников. Для каждого вычислили произведение длины на ширину.
Докажите, что сумма этих чисел равна произведению длины на ширину исходного
прямоугольника. б) Один прямоугольник лежит в другом (возможно, косо).
Докажите, что у внутреннего произведение длины на ширину меньше.


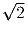 ускакала в бесконечность. Покрасим отрезки, где она побывала, а также
самый первый. Докажите, что кузнечик может из начала луча ускакать в
бесконечность прыжками некоторой постоянной длины C так, чтобы побывать в
точности на всех неокрашенных отрезках.
Задача 11:
Докажите, что площадь треугольника с вершинами в узлах сетки не менее
½.
Задача 12:
Стороны прямоугольника на шахматной доске параллельны сторонам доски.
Докажите, что разность суммарных площадей белых и черных частей
прямоугольника не превосходит площади одной клетки.
Задача 13:
Докажите неравенство для площади четырехугольника (a,b,c,d –
стороны по
порядку):
ускакала в бесконечность. Покрасим отрезки, где она побывала, а также
самый первый. Докажите, что кузнечик может из начала луча ускакать в
бесконечность прыжками некоторой постоянной длины C так, чтобы побывать в
точности на всех неокрашенных отрезках.
Задача 11:
Докажите, что площадь треугольника с вершинами в узлах сетки не менее
½.
Задача 12:
Стороны прямоугольника на шахматной доске параллельны сторонам доски.
Докажите, что разность суммарных площадей белых и черных частей
прямоугольника не превосходит площади одной клетки.
Задача 13:
Докажите неравенство для площади четырехугольника (a,b,c,d –
стороны по
порядку): 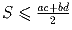 .
Задача 14:
(Принцип Кавальери)
а) На плоскости нарисованы два выпуклых многоугольника и прямая. Известно,
что любая прямая, параллельная данной, пересекается с многоугольниками по
отрезкам раной длины. Докажите, что эти многоугольники равновелики. б)
Докажите, что два равновеликих прямоугольника можно расположить на плоскости
так, что они будут пересекаться по равным отрезкам с любой прямой,
параллельной данной.
Задача 15:
(Корректность площади: решать, не используя понятия площади)
а) Прямоугольник разрезали на несколько меньших
прямоугольников. Для каждого вычислили произведение длины на ширину.
Докажите, что сумма этих чисел равна произведению длины на ширину исходного
прямоугольника. б) Один прямоугольник лежит в другом (возможно, косо).
Докажите, что у внутреннего произведение длины на ширину меньше.
.
Задача 14:
(Принцип Кавальери)
а) На плоскости нарисованы два выпуклых многоугольника и прямая. Известно,
что любая прямая, параллельная данной, пересекается с многоугольниками по
отрезкам раной длины. Докажите, что эти многоугольники равновелики. б)
Докажите, что два равновеликих прямоугольника можно расположить на плоскости
так, что они будут пересекаться по равным отрезкам с любой прямой,
параллельной данной.
Задача 15:
(Корректность площади: решать, не используя понятия площади)
а) Прямоугольник разрезали на несколько меньших
прямоугольников. Для каждого вычислили произведение длины на ширину.
Докажите, что сумма этих чисел равна произведению длины на ширину исходного
прямоугольника. б) Один прямоугольник лежит в другом (возможно, косо).
Докажите, что у внутреннего произведение длины на ширину меньше.