 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Делимость и остатки | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Делимость и остатки |
|
|
Задача 3: Делимое и делитель увеличили в три раза. Как изменятся неполное частное и остаток? Задача 4: Докажите, что остаток от деления простого числа на 30 – простое число или единица. Задача 5: Найдите остаток от деления
1999 • 2000 • 2001 + 2001³ на 7;
Задача 6: Найдите остаток от деления 9¹ºº на 8.
Задача 7: Найдите остаток от деления 12¹ºº на 13. Задача 8: Найдите остаток от деления 27 + 28 + 29 + 2¹º на 5. Задача 9: Найдите остаток при делении на 7 числа 100¹ºº – 30¹ºº. Задача 10: Найдите две последние цифры числа 1999²ººº;
Задача 11: Докажите, что
а) произведение 4 последовательных целых чисел;
б) разность квадратов двух простых чисел, больших 3,
делится на 24.
Задача 12: Докажите, что если a + 1 делится на 3, то 4 + 7a делится на 3.
Задача 13: Пусть n и m – натуральные числа, причем m ≠ 1. Известно, что
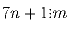 и
и 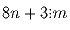 . Найдите m.
Решение:
Очевидно, что
. Найдите m.
Решение:
Очевидно, что 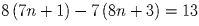 .
Следовательно, m = 13.
Задача 14:
Докажите, что из любых n целых чисел можно выбрать одно или несколько с
суммой, кратной n.
.
Следовательно, m = 13.
Задача 14:
Докажите, что из любых n целых чисел можно выбрать одно или несколько с
суммой, кратной n.Задача 15: Найдите остаток от деления 57 – 75 на 3.
Задача 16: Докажите, что 2343 + 43²³ делится на 66.
Задача 17: Найдите последнюю цифру числа
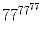 .
.Задача 18: Найдите две последние цифры числа 16²ººº. Задача 19: Докажите, что если a + 2 делится на 11 и 35 – b делится на 11, то a + b делится на 11.
Задача 20: Назовем автобусный билет с шестизначным номером счастливым, если сумма цифр его номера делится на 7. Могут ли два билета подряд быть счастливыми?
Задача 21: Шайка разбойников отобрала у купца мешок с монетами. Каждая монета стоит целое число грошей. Оказалось, что какую монету не отложи, оставшиеся монеты можно поделить между разбойниками так, что каждый получит одинаковую сумму. Докажите, что число монет без одной делится на число разбойников в шайке.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Делимость и остатки | Убрать решения |