 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Сравнения по модулю | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Сравнения по модулю |
|
|
Задача 2: Какой остаток при делении на 10 дает число a, если
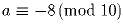 ?
?Задача 3: Найдите последнюю цифру числа 3999.
Задача 4: Докажите, что an – bn делится на a – b при любом натуральном n.
Задача 5: Докажите, что если n – нечётное число и a + b ≠ 0, то an + bn делится на a + b.
Задача 6: Докажите, что при любом натуральном n число
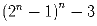 делится на 2n – 3.
делится на 2n – 3.Задача 7: Докажите, что при нечётных n и m число
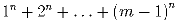 делится на m.
делится на m.Задача 8: Докажите, что а) при любом натуральном n 122n + 1 + 11n + 2 делится на 133;
б) при любых натуральных a и n число a2n + 1 + (a – 1)n + 2 делится на a² – a + 1.
Задача 9: Докажите, что 11¹ºº – 1 делится на 100.
Задача 10: Докажите, что
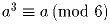 .
Задача 11:
Докажите, что для любого натурального n
.
Задача 11:
Докажите, что для любого натурального nа) либо 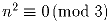 , либо
, либо
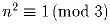 ;
;
б) либо 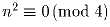 , либо
, либо
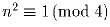 ;
;
в) либо 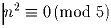 , либо
, либо
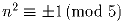 ;
;
г) либо  , либо
, либо
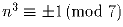 ;
;
д) либо 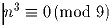 , либо
, либо
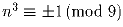 .
.
Задача 12: Докажите, что
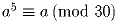 .
.Задача 13: Докажите, что уравнение 15x² – 7y² = 9 не имеет решений в целых числах.
Указание: Рассмотрите остатки при делении на 5.
Задача 14: Докажите, что уравнение x² – 7y = 10 не имеет решений в целых числах. Решение: Рассмотрите остатки при делении на 7.
Задача 15: Решите в целых числах уравнение x² + y² + z² = 8t – 1. Решение: Рассмотрев остатки при делении на 8, видим, что уравнение решений не имеет.
Задача 16: Докажите, что числа вида 103n + 1 нельзя представить в виде суммы двух кубов натуральных чисел. Решение: Рассмотрите остатки при делении на 7.
Задача 17: Доказать, что существует бесконечно много натуральных чисел, не представимых в виде суммы двух точных квадратов. Решение: Это числа вида n = 4k + 3.
Задача 18: Доказать, что существует бесконечно много натуральных чисел, не представимых в виде суммы трёх точных кубов. Решение: Это числа вида n = 9k + 4 и n = 9k + 5.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Сравнения по модулю | Убрать решения |