Задача 1: В деревне Вишкиль 9 домов. Из каждого дома тянется четыре шланга к четырём другим домам. Сколько шлангов в деревне?

Решение: 9 • 4/2 = 18

Задача 2: В москитной сетке ровно 100 узелков, любые два узелка соединены отдельной ниточкой. Сколько всего ниточек?

Решение:

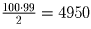
Задача 3: В доме отдыха Вишкиль 57 корпусов. Электрик решил соединить телефонными проводами каждый корпус ровно с пятью другими. Сможет ли он это сделать?

Задача 4: Существуют ли графы, степени вершин которых равны:

а) 9, 8, 8, 7, 6, 6, 3, 2, 1;

б) 8, 8, 7, 7, 6, 5, 4, 2, 1;

в) 8, 7, 6, 5, 4, 4, 3, 2, 1;

г) 8, 7, 5, 4, 4, 3, 2, 2, 2?

Решение: нет нет да нет

Задача 5: Докажите, что число людей, когда-либо живших на земле и сделавших нечётное число рукопожатий – чётно.

Задача 6: Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

Задача 7: Можно ли нарисовать на плоскости 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

Задача 8: В графе каждая вершина покрашена в синий или зеленый цвет. При этом каждая синяя вершина связана с пятью синими и десятью зелеными, а каждая зеленая – с девятью синими и шестью зелеными. Каких вершин больше – синих или зеленых?